
Question Number 121100 by Ar Brandon last updated on 05/Nov/20

Answered by TANMAY PANACEA last updated on 05/Nov/20
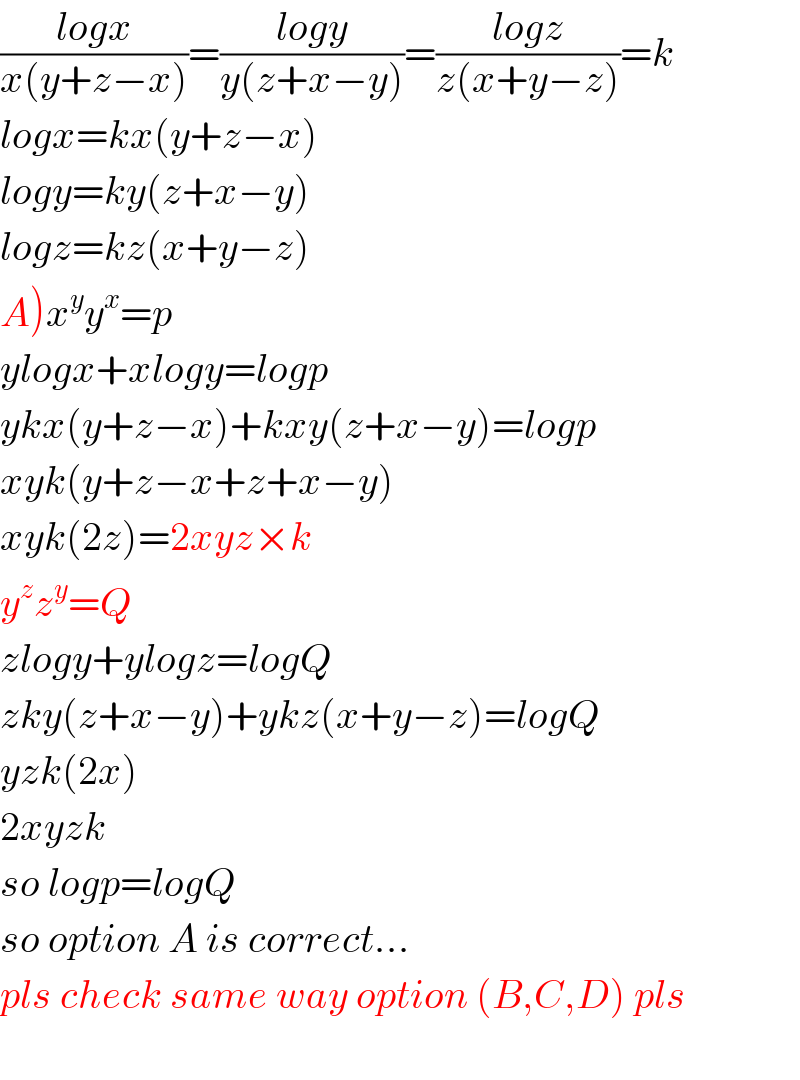
$$\frac{{logx}}{{x}\left({y}+{z}−{x}\right)}=\frac{{logy}}{{y}\left({z}+{x}−{y}\right)}=\frac{{logz}}{{z}\left({x}+{y}−{z}\right)}={k} \\ $$$${logx}={kx}\left({y}+{z}−{x}\right) \\ $$$${logy}={ky}\left({z}+{x}−{y}\right) \\ $$$${logz}={kz}\left({x}+{y}−{z}\right) \\ $$$$\left.{A}\right){x}^{{y}} {y}^{{x}} ={p} \\ $$$${ylogx}+{xlogy}={logp} \\ $$$${ykx}\left({y}+{z}−{x}\right)+{kxy}\left({z}+{x}−{y}\right)={logp} \\ $$$${xyk}\left({y}+{z}−{x}+{z}+{x}−{y}\right) \\ $$$${xyk}\left(\mathrm{2}{z}\right)=\mathrm{2}{xyz}×{k} \\ $$$${y}^{{z}} {z}^{{y}} ={Q} \\ $$$${zlogy}+{ylogz}={logQ} \\ $$$${zky}\left({z}+{x}−{y}\right)+{ykz}\left({x}+{y}−{z}\right)={logQ} \\ $$$${yzk}\left(\mathrm{2}{x}\right) \\ $$$$\mathrm{2}{xyzk} \\ $$$${so}\:{logp}={logQ} \\ $$$${so}\:{option}\:{A}\:{is}\:{correct}... \\ $$$${pls}\:{check}\:{same}\:{way}\:{option}\:\left({B},{C},{D}\right)\:{pls} \\ $$$$ \\ $$
Commented by Ar Brandon last updated on 05/Nov/20
Thank you Sir. It is a multiple correct choice type question.
Commented by TANMAY PANACEA last updated on 05/Nov/20
$${most}\:{welcome}\:{sir} \\ $$
