Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

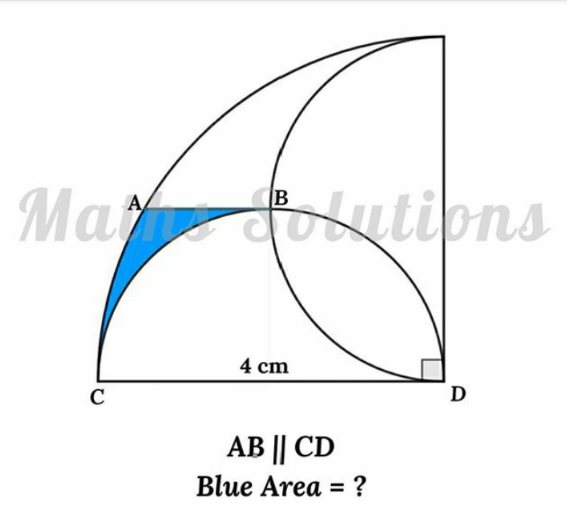
Question Number 120864 by mnjuly1970 last updated on 03/Nov/20

Commented by math35 last updated on 03/Nov/20

please sir how was the diagram made

$${please}\:{sir}\:{how}\:{was}\:{the} \\ $$$${diagram}\:{made} \\ $$

Commented by mnjuly1970 last updated on 03/Nov/20

hello sir Tanmay: I took a photo of the chart and sent it.using the attach image option. have a nice time...

$${hello}\:{sir}\:{Tanmay}: \\ $$$${I}\:{took}\:{a}\:{photo}\:{of}\:{the}\:{chart}\: \\ $$$$\:{and}\:{sent}\:{it}.{using}\:{the}\:{attach}\:{image} \\ $$$${option}.\:{have}\:{a}\:{nice}\:{time}... \\ $$

Commented by TANMAY PANACEA last updated on 03/Nov/20

pls chk my answer...i do not remember formula

$${pls}\:{chk}\:{my}\:{answer}...{i}\:{do}\:{not}\:{remember}\:{formula} \\ $$

Answered by TANMAY PANACEA last updated on 03/Nov/20

D is origin(0,0) C(−4,0) eqn of big semi circle→x^2 +y^2 =4^2 mid point C and D (−2,0) eqn of small semi circle centre(−2,0) and radius 2 (x+2)^2 +y^2 =2^2 eqn another small semi circle x^2 +(y−2)^2 =2^2 solve x^2 +4x+4+y^2 =4 x^2 +y^2 −4y+4=4 −4x−4y=0→x=−y so x^2 +4x+4+x^2 =4→2x^2 +4x=0 2x(x+2)=0 so point B(−2,2) eqn AB is y=2 point A ...solve y=2 and x^2 +y^2 =4^2 x^2 =16−4=12→x=±2(√3) point A(−2(√3) ,2) required area {∫_(−4) ^(−2(√3)) (√(16−x^2 )) dx+∫_(−2(√3) ) ^(−2) 2dx}−{∫_(−4) ^(−2) (√(4−(x+2)^2 )) dx} pls chk ∫(√(a^2 −x^2 )) dx=(x/2)(√(a^2 −x^2 )) +(a^2 /2)sin^(−1) ((x/a)) I_1 =∣(x/2)(√(16−x^2 )) +((16)/2)sin^(−1) ((x/4))∣_(−4) ^(−2(√3) ) =(((−2(√3))/2)(√(16−12)) +8sin^(−1) (((−2(√3))/4)) =−(√3) ×2+8(−(π/3))=−2(√3) −((8π)/3) I_2 =2∣x∣_(−2(√3)) ^(−2) =2(−2+2(√3) )=4(√3) −4 ★∫_(−4) ^(−2) (√(4−(x+2)^2 )) dx (x+2)=p ∫_(−2) ^0 (√(2^2 −p^2 )) dp=∣(p/2)(√(2^2 −p^2 )) +(4/2)sin^(−1) ((p/2))∣_(−2) ^0 =(0)−{((−2)/2)(√(4−4)) +2sin^(−1) (((−2)/2))} =0−0−2sin^(−1) (−1)=−2×((−π)/2)=π rewuired answer I_1 +I_2 −I_3 =(−2(√3) −((8π)/3))+(4(√3) −4)−(π) =2(√3) −4−((11π)/3)

$${D}\:{is}\:{origin}\left(\mathrm{0},\mathrm{0}\right)\:\:{C}\left(−\mathrm{4},\mathrm{0}\right) \\ $$$${eqn}\:{of}\:{big}\:{semi}\:{circle}\rightarrow{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{4}^{\mathrm{2}} \\ $$$${mid}\:{point}\:{C}\:{and}\:{D}\:\left(−\mathrm{2},\mathrm{0}\right) \\ $$$${eqn}\:{of}\:{small}\:{semi}\:{circle}\:{centre}\left(−\mathrm{2},\mathrm{0}\right)\:{and}\:{radius}\:\mathrm{2} \\ $$$$\left({x}+\mathrm{2}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{2}^{\mathrm{2}} \\ $$$${eqn}\:{another}\:{small}\:{semi}\:{circle}\:{x}^{\mathrm{2}} +\left({y}−\mathrm{2}\right)^{\mathrm{2}} =\mathrm{2}^{\mathrm{2}} \\ $$$${solve}\:\:{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{4}+{y}^{\mathrm{2}} =\mathrm{4} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{4}{y}+\mathrm{4}=\mathrm{4} \\ $$$$−\mathrm{4}{x}−\mathrm{4}{y}=\mathrm{0}\rightarrow{x}=−{y} \\ $$$${so}\:{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{4}+{x}^{\mathrm{2}} =\mathrm{4}\rightarrow\mathrm{2}{x}^{\mathrm{2}} +\mathrm{4}{x}=\mathrm{0}\:\:\:\mathrm{2}{x}\left({x}+\mathrm{2}\right)=\mathrm{0} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{point}}\:\boldsymbol{{B}}\left(−\mathrm{2},\mathrm{2}\right) \\ $$$${eqn}\:\:{AB}\:{is}\:{y}=\mathrm{2} \\ $$$${point}\:{A}\:...{solve}\:{y}=\mathrm{2}\:{and}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{4}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} =\mathrm{16}−\mathrm{4}=\mathrm{12}\rightarrow{x}=\pm\mathrm{2}\sqrt{\mathrm{3}}\: \\ $$$$\boldsymbol{{point}}\:\boldsymbol{{A}}\left(−\mathrm{2}\sqrt{\mathrm{3}}\:,\mathrm{2}\right) \\ $$$${required}\:{area} \\ $$$$\left\{\int_{−\mathrm{4}} ^{−\mathrm{2}\sqrt{\mathrm{3}}} \sqrt{\mathrm{16}−{x}^{\mathrm{2}} }\:{dx}+\int_{−\mathrm{2}\sqrt{\mathrm{3}}\:} ^{−\mathrm{2}} \mathrm{2}{dx}\right\}−\left\{\int_{−\mathrm{4}} ^{−\mathrm{2}} \sqrt{\mathrm{4}−\left({x}+\mathrm{2}\right)^{\mathrm{2}} }\:{dx}\right\} \\ $$$${pls}\:{chk} \\ $$$$\int\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }\:{dx}=\frac{{x}}{\mathrm{2}}\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} \:}\:+\frac{{a}^{\mathrm{2}} }{\mathrm{2}}{sin}^{−\mathrm{1}} \left(\frac{{x}}{{a}}\right) \\ $$$${I}_{\mathrm{1}} =\mid\frac{{x}}{\mathrm{2}}\sqrt{\mathrm{16}−{x}^{\mathrm{2}} }\:+\frac{\mathrm{16}}{\mathrm{2}}{sin}^{−\mathrm{1}} \left(\frac{{x}}{\mathrm{4}}\right)\mid_{−\mathrm{4}} ^{−\mathrm{2}\sqrt{\mathrm{3}}\:} \\ $$$$=\left(\frac{−\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{2}}\sqrt{\mathrm{16}−\mathrm{12}}\:+\mathrm{8}{sin}^{−\mathrm{1}} \left(\frac{−\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{4}}\right)\right. \\ $$$$=−\sqrt{\mathrm{3}}\:×\mathrm{2}+\mathrm{8}\left(−\frac{\pi}{\mathrm{3}}\right)=−\mathrm{2}\sqrt{\mathrm{3}}\:−\frac{\mathrm{8}\pi}{\mathrm{3}} \\ $$$${I}_{\mathrm{2}} =\mathrm{2}\mid{x}\mid_{−\mathrm{2}\sqrt{\mathrm{3}}} ^{−\mathrm{2}} =\mathrm{2}\left(−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{3}}\:\right)=\mathrm{4}\sqrt{\mathrm{3}}\:−\mathrm{4} \\ $$$$\bigstar\int_{−\mathrm{4}} ^{−\mathrm{2}} \sqrt{\mathrm{4}−\left({x}+\mathrm{2}\right)^{\mathrm{2}} }\:{dx} \\ $$$$\left({x}+\mathrm{2}\right)={p} \\ $$$$\int_{−\mathrm{2}} ^{\mathrm{0}} \sqrt{\mathrm{2}^{\mathrm{2}} −{p}^{\mathrm{2}} }\:{dp}=\mid\frac{{p}}{\mathrm{2}}\sqrt{\mathrm{2}^{\mathrm{2}} −{p}^{\mathrm{2}} }\:+\frac{\mathrm{4}}{\mathrm{2}}{sin}^{−\mathrm{1}} \left(\frac{{p}}{\mathrm{2}}\right)\mid_{−\mathrm{2}} ^{\mathrm{0}} \\ $$$$=\left(\mathrm{0}\right)−\left\{\frac{−\mathrm{2}}{\mathrm{2}}\sqrt{\mathrm{4}−\mathrm{4}}\:+\mathrm{2}{sin}^{−\mathrm{1}} \left(\frac{−\mathrm{2}}{\mathrm{2}}\right)\right\} \\ $$$$=\mathrm{0}−\mathrm{0}−\mathrm{2}{sin}^{−\mathrm{1}} \left(−\mathrm{1}\right)=−\mathrm{2}×\frac{−\pi}{\mathrm{2}}=\pi \\ $$$${rewuired}\:{answer} \\ $$$${I}_{\mathrm{1}} +{I}_{\mathrm{2}} −{I}_{\mathrm{3}} \\ $$$$=\left(−\mathrm{2}\sqrt{\mathrm{3}}\:−\frac{\mathrm{8}\pi}{\mathrm{3}}\right)+\left(\mathrm{4}\sqrt{\mathrm{3}}\:−\mathrm{4}\right)−\left(\pi\right) \\ $$$$=\mathrm{2}\sqrt{\mathrm{3}}\:−\mathrm{4}−\frac{\mathrm{11}\pi}{\mathrm{3}} \\ $$

Commented by TANMAY PANACEA last updated on 03/Nov/20

Terms of Service

Privacy Policy

Contact: info@tinkutara.com