
Question Number 120801 by TITA last updated on 02/Nov/20

Commented by liberty last updated on 02/Nov/20
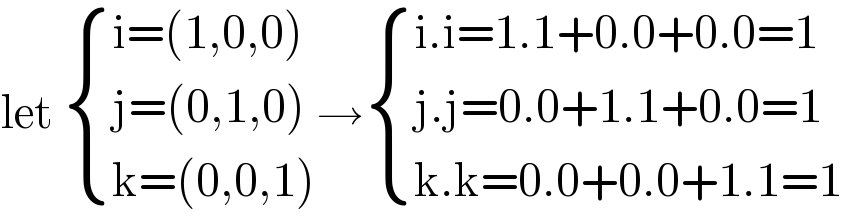
$$\mathrm{let}\:\begin{cases}{\mathrm{i}=\left(\mathrm{1},\mathrm{0},\mathrm{0}\right)}\\{\mathrm{j}=\left(\mathrm{0},\mathrm{1},\mathrm{0}\right)}\\{\mathrm{k}=\left(\mathrm{0},\mathrm{0},\mathrm{1}\right)}\end{cases}\rightarrow\begin{cases}{\mathrm{i}.\mathrm{i}=\mathrm{1}.\mathrm{1}+\mathrm{0}.\mathrm{0}+\mathrm{0}.\mathrm{0}=\mathrm{1}}\\{\mathrm{j}.\mathrm{j}=\mathrm{0}.\mathrm{0}+\mathrm{1}.\mathrm{1}+\mathrm{0}.\mathrm{0}=\mathrm{1}}\\{\mathrm{k}.\mathrm{k}=\mathrm{0}.\mathrm{0}+\mathrm{0}.\mathrm{0}+\mathrm{1}.\mathrm{1}=\mathrm{1}}\end{cases} \\ $$
Commented by TITA last updated on 03/Nov/20

$${thanks} \\ $$
Answered by $@y@m last updated on 03/Nov/20
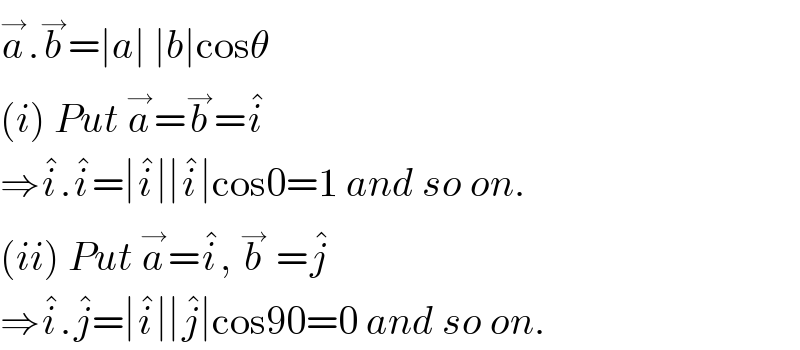
$$\overset{\rightarrow} {{a}}.\overset{\rightarrow} {{b}}=\mid{a}\mid\:\mid{b}\mid\mathrm{cos}\theta \\ $$$$\left({i}\right)\:{Put}\:\overset{\rightarrow} {{a}}=\overset{\rightarrow} {{b}}=\hat {{i}} \\ $$$$\Rightarrow\hat {{i}}.\hat {{i}}=\mid\hat {{i}}\mid\mid\hat {{i}}\mid\mathrm{cos0}=\mathrm{1}\:{and}\:{so}\:{on}. \\ $$$$\left({ii}\right)\:{Put}\:\overset{\rightarrow} {{a}}=\hat {{i}},\:\overset{\rightarrow} {{b}}\:=\hat {{j}} \\ $$$$\Rightarrow\hat {{i}}.\hat {{j}}=\mid\hat {{i}}\mid\mid\hat {{j}}\mid\mathrm{cos90}=\mathrm{0}\:{and}\:{so}\:{on}. \\ $$
Commented by TITA last updated on 03/Nov/20

$${thanks} \\ $$
