Question and Answers Forum

All Questions      Topic List

Mensuration Questions

Previous in All Question      Next in All Question      

Previous in Mensuration      Next in Mensuration      

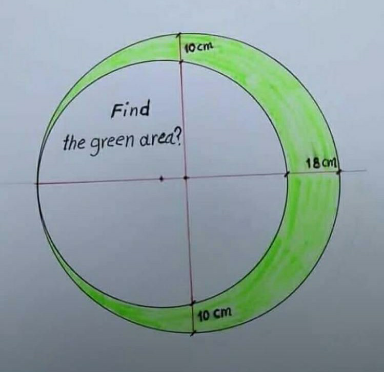
Question Number 120790 by peter frank last updated on 02/Nov/20

Commented by TANMAY PANACEA last updated on 02/Nov/20

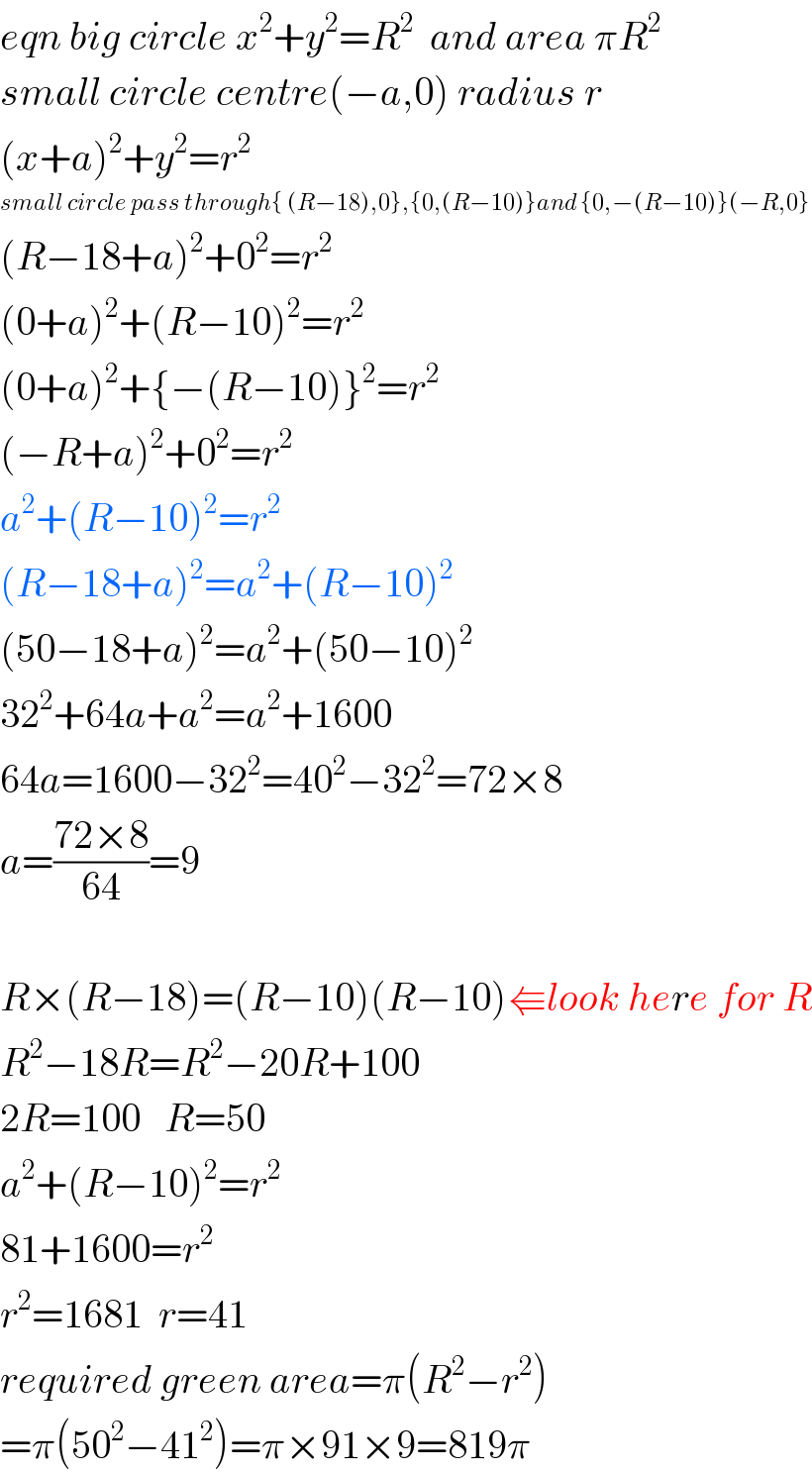
eqn big circle x^2 +y^2 =R^2 and area πR^2 small circle centre(−a,0) radius r (x+a)^2 +y^2 =r^2 small circle pass through{ (R−18),0},{0,(R−10)}and {0,−(R−10)}(−R,0} (R−18+a)^2 +0^2 =r^2 (0+a)^2 +(R−10)^2 =r^2 (0+a)^2 +{−(R−10)}^2 =r^2 (−R+a)^2 +0^2 =r^2 a^2 +(R−10)^2 =r^2 (R−18+a)^2 =a^2 +(R−10)^2 (50−18+a)^2 =a^2 +(50−10)^2 32^2 +64a+a^2 =a^2 +1600 64a=1600−32^2 =40^2 −32^2 =72×8 a=((72×8)/(64))=9 R×(R−18)=(R−10)(R−10)⇚look here for R R^2 −18R=R^2 −20R+100 2R=100 R=50 a^2 +(R−10)^2 =r^2 81+1600=r^2 r^2 =1681 r=41 required green area=π(R^2 −r^2 ) =π(50^2 −41^2 )=π×91×9=819π

$${eqn}\:{big}\:{circle}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={R}^{\mathrm{2}} \:\:{and}\:{area}\:\pi{R}^{\mathrm{2}} \\ $$$${small}\:{circle}\:{centre}\left(−{a},\mathrm{0}\right)\:{radius}\:{r} \\ $$$$\left({x}+{a}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$${small}\:{circle}\:{pass}\:{through}\left\{\:\left({R}−\mathrm{18}\right),\mathrm{0}\right\},\left\{\mathrm{0},\left({R}−\mathrm{10}\right)\right\}{and}\:\left\{\mathrm{0},−\left({R}−\mathrm{10}\right)\right\}\left(−{R},\mathrm{0}\right\} \\ $$$$\left({R}−\mathrm{18}+{a}\right)^{\mathrm{2}} +\mathrm{0}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\left(\mathrm{0}+{a}\right)^{\mathrm{2}} +\left({R}−\mathrm{10}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\left(\mathrm{0}+{a}\right)^{\mathrm{2}} +\left\{−\left({R}−\mathrm{10}\right)\right\}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\left(−{R}+{a}\right)^{\mathrm{2}} +\mathrm{0}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} +\left({R}−\mathrm{10}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\left({R}−\mathrm{18}+{a}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} +\left({R}−\mathrm{10}\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{50}−\mathrm{18}+{a}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} +\left(\mathrm{50}−\mathrm{10}\right)^{\mathrm{2}} \\ $$$$\mathrm{32}^{\mathrm{2}} +\mathrm{64}{a}+{a}^{\mathrm{2}} ={a}^{\mathrm{2}} +\mathrm{1600} \\ $$$$\mathrm{64}{a}=\mathrm{1600}−\mathrm{32}^{\mathrm{2}} =\mathrm{40}^{\mathrm{2}} −\mathrm{32}^{\mathrm{2}} =\mathrm{72}×\mathrm{8} \\ $$$${a}=\frac{\mathrm{72}×\mathrm{8}}{\mathrm{64}}=\mathrm{9} \\ $$$$ \\ $$$${R}×\left({R}−\mathrm{18}\right)=\left({R}−\mathrm{10}\right)\left({R}−\mathrm{10}\right)\Lleftarrow{look}\:{here}\:{for}\:{R} \\ $$$${R}^{\mathrm{2}} −\mathrm{18}{R}={R}^{\mathrm{2}} −\mathrm{20}{R}+\mathrm{100} \\ $$$$\mathrm{2}{R}=\mathrm{100}\:\:\:{R}=\mathrm{50} \\ $$$${a}^{\mathrm{2}} +\left({R}−\mathrm{10}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\mathrm{81}+\mathrm{1600}={r}^{\mathrm{2}} \\ $$$${r}^{\mathrm{2}} =\mathrm{1681}\:\:{r}=\mathrm{41} \\ $$$${required}\:{green}\:{area}=\pi\left({R}^{\mathrm{2}} −{r}^{\mathrm{2}} \right) \\ $$$$=\pi\left(\mathrm{50}^{\mathrm{2}} −\mathrm{41}^{\mathrm{2}} \right)=\pi×\mathrm{91}×\mathrm{9}=\mathrm{819}\pi \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com