Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 120560 by peter frank last updated on 01/Nov/20

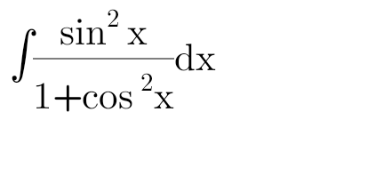
Answered by mathmax by abdo last updated on 01/Nov/20

I=∫ ((sin^2 x)/(1+cos^2 x))dx ⇒I =∫ (((1−cos(2x))/2)/(1+((1+cos(2x))/2)))dx =∫ ((2−cos(2x))/(3+cos(2x)))dx =_(tanx=t) ∫ ((2−((1−t^2 )/(1+t^2 )))/(3+((1−t^2 )/(1+t^2 ))))dt =∫ ((2+2t^2 −1+t^2 )/(3+3t^2 +1−t^2 ))dt =∫ ((3t^2 +1)/(2t^2 +4))dt =(1/2)∫ ((3t^2 +1)/(t^2 +2))dt =(1/2)∫ ((3(t^2 +2)−5)/(t^2 +2))dt =(3/2)t −(5/2)∫ (dt/(t^2 +2))(→t=(√2)u) =((3t)/2)−(5/2)∫ (((√2)du)/(2(1+u^2 ))) =((3t)/2)−((5(√2))/4) arctanu +C ⇒ I=(3/2)tanx −((5(√2))/4)arctan(((tanx)/( (√2)))) +C

$$\mathrm{I}=\int\:\:\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{x}}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\mathrm{dx}\:\Rightarrow\mathrm{I}\:=\int\:\:\frac{\frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{2}}}{\mathrm{1}+\frac{\mathrm{1}+\mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{2}}}\mathrm{dx}\:=\int\:\:\frac{\mathrm{2}−\mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{3}+\mathrm{cos}\left(\mathrm{2x}\right)}\mathrm{dx} \\ $$$$=_{\mathrm{tanx}=\mathrm{t}} \:\:\:\:\int\:\:\frac{\mathrm{2}−\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}{\mathrm{3}+\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}\mathrm{dt}\:=\int\:\:\frac{\mathrm{2}+\mathrm{2t}^{\mathrm{2}} −\mathrm{1}+\mathrm{t}^{\mathrm{2}} }{\mathrm{3}+\mathrm{3t}^{\mathrm{2}} +\mathrm{1}−\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:=\int\:\:\frac{\mathrm{3t}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2t}^{\mathrm{2}} +\mathrm{4}}\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{\mathrm{3t}^{\mathrm{2}} \:+\mathrm{1}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{2}}\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{\mathrm{3}\left(\mathrm{t}^{\mathrm{2}} +\mathrm{2}\right)−\mathrm{5}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{2}}\mathrm{dt}\:=\frac{\mathrm{3}}{\mathrm{2}}\mathrm{t}\:−\frac{\mathrm{5}}{\mathrm{2}}\int\:\:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{2}}\left(\rightarrow\mathrm{t}=\sqrt{\mathrm{2}}\mathrm{u}\right) \\ $$$$=\frac{\mathrm{3t}}{\mathrm{2}}−\frac{\mathrm{5}}{\mathrm{2}}\int\:\:\frac{\sqrt{\mathrm{2}}\mathrm{du}}{\mathrm{2}\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)}\:=\frac{\mathrm{3t}}{\mathrm{2}}−\frac{\mathrm{5}\sqrt{\mathrm{2}}}{\mathrm{4}}\:\mathrm{arctanu}\:+\mathrm{C}\:\Rightarrow \\ $$$$\mathrm{I}=\frac{\mathrm{3}}{\mathrm{2}}\mathrm{tanx}\:−\frac{\mathrm{5}\sqrt{\mathrm{2}}}{\mathrm{4}}\mathrm{arctan}\left(\frac{\mathrm{tanx}}{\:\sqrt{\mathrm{2}}}\right)\:+\mathrm{C} \\ $$$$ \\ $$

Commented by peter frank last updated on 01/Nov/20

thank you

$$\mathrm{thank}\:\mathrm{you} \\ $$

Answered by MJS_new last updated on 01/Nov/20

∫((sin^2 x)/(1+cos^2 x))dx=∫((2/(1+cos^2 x))−1)dx 2∫(dx/(1+cos^2 x))= [t=tan x → dx=cos^2 x dx] =2∫(dt/(t^2 +2))=(√2)arctan (((√2)t)/2) = =(√2)arctan (((√2)tan x)/2) ∫((sin^2 x)/(1+cos^2 x))dx=−x+(√2)arctan (((√2)tan x)/2) +C

$$\int\frac{\mathrm{sin}^{\mathrm{2}} \:{x}}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:{x}}{dx}=\int\left(\frac{\mathrm{2}}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:{x}}−\mathrm{1}\right){dx} \\ $$$$\mathrm{2}\int\frac{{dx}}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:{x}}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:{x}\:\rightarrow\:{dx}=\mathrm{cos}^{\mathrm{2}} \:{x}\:{dx}\right] \\ $$$$=\mathrm{2}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{2}}=\sqrt{\mathrm{2}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{2}}{t}}{\mathrm{2}}\:= \\ $$$$=\sqrt{\mathrm{2}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{2}}\mathrm{tan}\:{x}}{\mathrm{2}} \\ $$$$\int\frac{\mathrm{sin}^{\mathrm{2}} \:{x}}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:{x}}{dx}=−{x}+\sqrt{\mathrm{2}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{2}}\mathrm{tan}\:{x}}{\mathrm{2}}\:+{C} \\ $$

Commented by peter frank last updated on 01/Nov/20

thank you

$$\mathrm{thank}\:\mathrm{you} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com