Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 120558 by peter frank last updated on 01/Nov/20

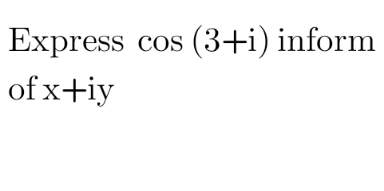
Answered by mr W last updated on 01/Nov/20

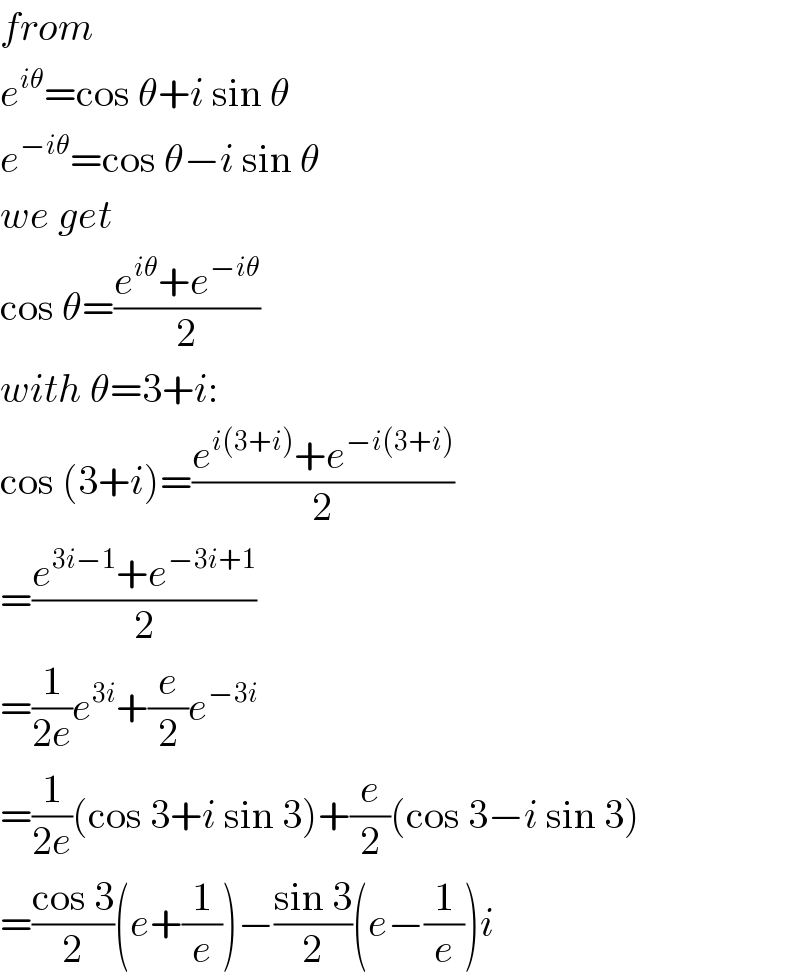
from e^(iθ) =cos θ+i sin θ e^(−iθ) =cos θ−i sin θ we get cos θ=((e^(iθ) +e^(−iθ) )/2) with θ=3+i: cos (3+i)=((e^(i(3+i)) +e^(−i(3+i)) )/2) =((e^(3i−1) +e^(−3i+1) )/2) =(1/(2e))e^(3i) +(e/2)e^(−3i) =(1/(2e))(cos 3+i sin 3)+(e/2)(cos 3−i sin 3) =((cos 3)/2)(e+(1/e))−((sin 3)/2)(e−(1/e))i

$${from} \\ $$$${e}^{{i}\theta} =\mathrm{cos}\:\theta+{i}\:\mathrm{sin}\:\theta \\ $$$${e}^{−{i}\theta} =\mathrm{cos}\:\theta−{i}\:\mathrm{sin}\:\theta \\ $$$${we}\:{get} \\ $$$$\mathrm{cos}\:\theta=\frac{{e}^{{i}\theta} +{e}^{−{i}\theta} }{\mathrm{2}} \\ $$$${with}\:\theta=\mathrm{3}+{i}: \\ $$$$\mathrm{cos}\:\left(\mathrm{3}+{i}\right)=\frac{{e}^{{i}\left(\mathrm{3}+{i}\right)} +{e}^{−{i}\left(\mathrm{3}+{i}\right)} }{\mathrm{2}} \\ $$$$=\frac{{e}^{\mathrm{3}{i}−\mathrm{1}} +{e}^{−\mathrm{3}{i}+\mathrm{1}} }{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{e}}{e}^{\mathrm{3}{i}} +\frac{{e}}{\mathrm{2}}{e}^{−\mathrm{3}{i}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{e}}\left(\mathrm{cos}\:\mathrm{3}+{i}\:\mathrm{sin}\:\mathrm{3}\right)+\frac{{e}}{\mathrm{2}}\left(\mathrm{cos}\:\mathrm{3}−{i}\:\mathrm{sin}\:\mathrm{3}\right) \\ $$$$=\frac{\mathrm{cos}\:\mathrm{3}}{\mathrm{2}}\left({e}+\frac{\mathrm{1}}{{e}}\right)−\frac{\mathrm{sin}\:\mathrm{3}}{\mathrm{2}}\left({e}−\frac{\mathrm{1}}{{e}}\right){i} \\ $$

Commented by peter frank last updated on 01/Nov/20

thank you

$$\mathrm{thank}\:\mathrm{you} \\ $$

Answered by TANMAY PANACEA last updated on 01/Nov/20

cos3cosi−sin3sini cos3cosh−sin3×isinh

$${cos}\mathrm{3}{cosi}−{sin}\mathrm{3}{sini} \\ $$$${cos}\mathrm{3}{cosh}−{sin}\mathrm{3}×{isinh} \\ $$

Answered by mathmax by abdo last updated on 01/Nov/20

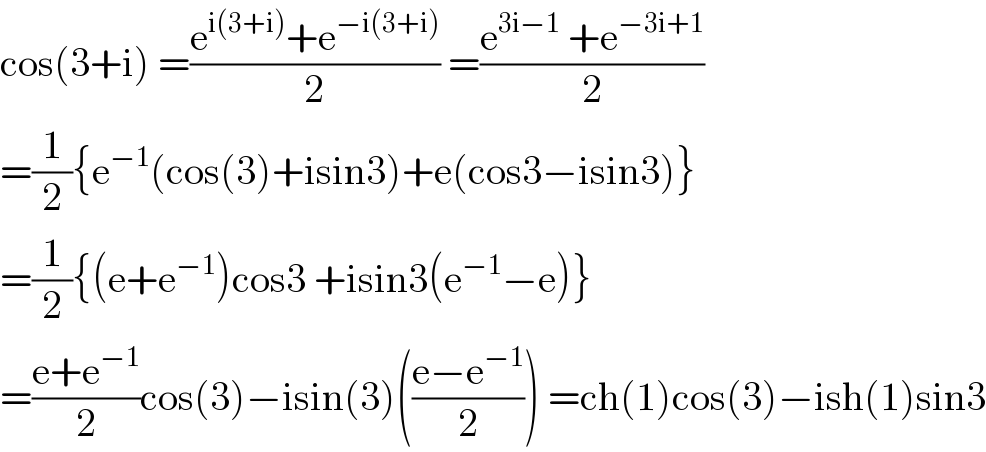
cos(3+i) =((e^(i(3+i)) +e^(−i(3+i)) )/2) =((e^(3i−1) +e^(−3i+1) )/2) =(1/2){e^(−1) (cos(3)+isin3)+e(cos3−isin3)} =(1/2){(e+e^(−1) )cos3 +isin3(e^(−1) −e)} =((e+e^(−1) )/2)cos(3)−isin(3)(((e−e^(−1) )/2)) =ch(1)cos(3)−ish(1)sin3

$$\mathrm{cos}\left(\mathrm{3}+\mathrm{i}\right)\:=\frac{\mathrm{e}^{\mathrm{i}\left(\mathrm{3}+\mathrm{i}\right)} +\mathrm{e}^{−\mathrm{i}\left(\mathrm{3}+\mathrm{i}\right)} }{\mathrm{2}}\:=\frac{\mathrm{e}^{\mathrm{3i}−\mathrm{1}} \:+\mathrm{e}^{−\mathrm{3i}+\mathrm{1}} }{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{e}^{−\mathrm{1}} \left(\mathrm{cos}\left(\mathrm{3}\right)+\mathrm{isin3}\right)+\mathrm{e}\left(\mathrm{cos3}−\mathrm{isin3}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\left(\mathrm{e}+\mathrm{e}^{−\mathrm{1}} \right)\mathrm{cos3}\:+\mathrm{isin3}\left(\mathrm{e}^{−\mathrm{1}} −\mathrm{e}\right)\right\} \\ $$$$=\frac{\mathrm{e}+\mathrm{e}^{−\mathrm{1}} }{\mathrm{2}}\mathrm{cos}\left(\mathrm{3}\right)−\mathrm{isin}\left(\mathrm{3}\right)\left(\frac{\mathrm{e}−\mathrm{e}^{−\mathrm{1}} }{\mathrm{2}}\right)\:=\mathrm{ch}\left(\mathrm{1}\right)\mathrm{cos}\left(\mathrm{3}\right)−\mathrm{ish}\left(\mathrm{1}\right)\mathrm{sin3} \\ $$

Commented by peter frank last updated on 01/Nov/20

thank you

$$\mathrm{thank}\:\:\mathrm{you} \\ $$

Commented by mathmax by abdo last updated on 08/Nov/20

you are welcome

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com