
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 120431 by john santu last updated on 31/Oct/20

Commented by john santu last updated on 31/Oct/20
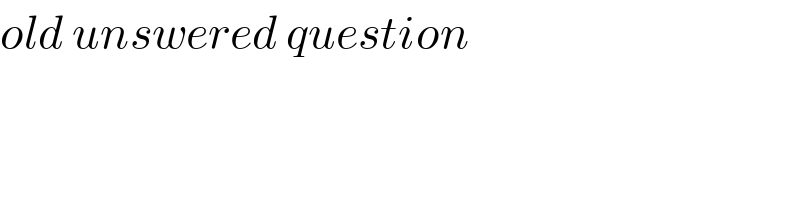
$${old}\:{unswered}\:{question} \\ $$
Commented by mr W last updated on 31/Oct/20

$${question}\:{is}\:{not}\:{quite}\:{clear}\:{for}\:{me}. \\ $$$${according}\:{to}\:{my}\:{understanding}\:{a} \\ $$$${memorable}\:{number}\:{is}\:{e}.{g}. \\ $$$$\mathrm{123}−\mathrm{1234}\:{or}\:\mathrm{123}−\mathrm{4123}. \\ $$$${so}\:{my}\:{answer}\:{is} \\ $$$$\mathrm{2}×{C}_{\mathrm{3}} ^{\mathrm{10}} ×\mathrm{3}!×\mathrm{7}=\mathrm{10080} \\ $$
Answered by john santu last updated on 31/Oct/20

$${Let}\:{A}\:{denote}\:{the}\:{set}\:{of}\:{telephone}\:{numbers} \\ $$$${for}\:{which}\:{d}_{\mathrm{1}} {d}_{\mathrm{2}} {d}_{\mathrm{3}} \:{is}\:{the}\:{same}\:{as}\:{d}_{\mathrm{4}} {d}_{\mathrm{5}} {d}_{\mathrm{6}} \\ $$$${and}\:{let}\:{B}\:{the}\:{set}\:{of}\:{telephone}\:{numbers}\: \\ $$$${for}\:{which}\:{d}_{\mathrm{1}} {d}_{\mathrm{2}} {d}_{\mathrm{3}} \:{concides}\:{with}\:{d}_{\mathrm{5}} {d}_{\mathrm{6}} {d}_{\mathrm{7}} . \\ $$$${A}\:{telephone}\:{number}\:{d}_{\mathrm{1}} {d}_{\mathrm{2}} {d}_{\mathrm{3}} −{d}_{\mathrm{4}} {d}_{\mathrm{5}} {d}_{\mathrm{6}} {d}_{\mathrm{7}} \\ $$$${belong}\:{to}\:{A}\cap{B}\:{if}\:{only}\:{if}\:{d}_{\mathrm{1}} ={d}_{\mathrm{2}} ={d}_{\mathrm{3}} ={d}_{\mathrm{4}} =...={d}_{\mathrm{7}} . \\ $$$${Hence}\:{n}\left({A}\cap{B}\right)=\mathrm{10}.\:{Thus}\:{by}\:{Inclusion}−{Exclusion}\:{Principle} \\ $$$${n}\left({A}\cup{B}\right)={n}\left({A}\right)+{n}\left({B}\right)−{n}\left({A}\cap{B}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{10}^{\mathrm{3}} .\mathrm{1}.\mathrm{10}\:+\:\mathrm{10}^{\mathrm{3}} .\mathrm{10}.\mathrm{1}−\mathrm{10} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{20},\mathrm{000}−\mathrm{10}=\mathrm{19},\mathrm{990} \\ $$
