
Question Number 120389 by help last updated on 31/Oct/20

Commented by help last updated on 31/Oct/20

$${question}\:\mathrm{2}{a} \\ $$
Commented by help last updated on 31/Oct/20

$${question}\:\mathrm{3}{a}\:{pls} \\ $$
Answered by Dwaipayan Shikari last updated on 31/Oct/20
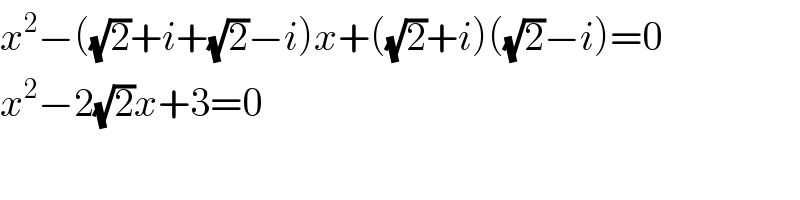
$${x}^{\mathrm{2}} −\left(\sqrt{\mathrm{2}}+{i}+\sqrt{\mathrm{2}}−{i}\right){x}+\left(\sqrt{\mathrm{2}}+{i}\right)\left(\sqrt{\mathrm{2}}−{i}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{2}}{x}+\mathrm{3}=\mathrm{0} \\ $$
Answered by bramlexs22 last updated on 31/Oct/20
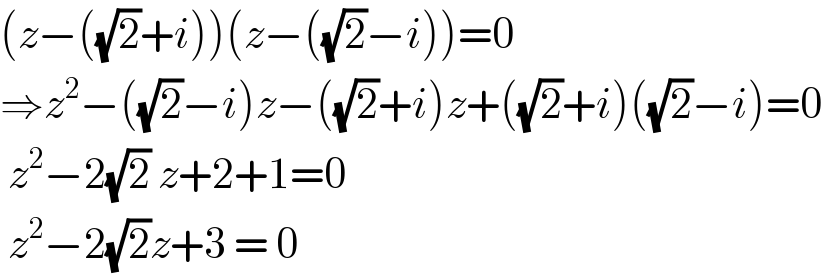
$$\left({z}−\left(\sqrt{\mathrm{2}}+{i}\right)\right)\left({z}−\left(\sqrt{\mathrm{2}}−{i}\right)\right)=\mathrm{0} \\ $$$$\Rightarrow{z}^{\mathrm{2}} −\left(\sqrt{\mathrm{2}}−{i}\right){z}−\left(\sqrt{\mathrm{2}}+{i}\right){z}+\left(\sqrt{\mathrm{2}}+{i}\right)\left(\sqrt{\mathrm{2}}−{i}\right)=\mathrm{0} \\ $$$$\:{z}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{2}}\:{z}+\mathrm{2}+\mathrm{1}=\mathrm{0} \\ $$$$\:{z}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{2}}{z}+\mathrm{3}\:=\:\mathrm{0} \\ $$
Answered by ebi last updated on 31/Oct/20
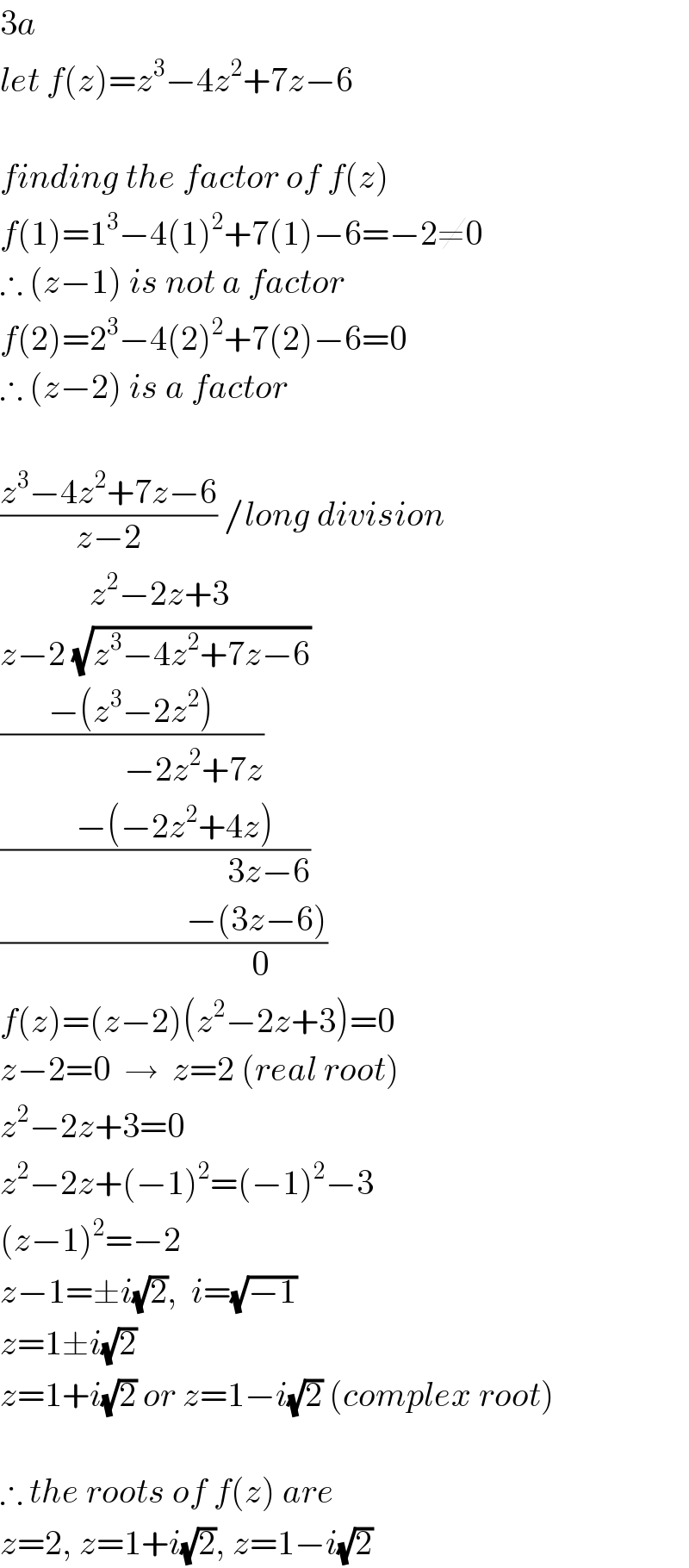
$$\mathrm{3}{a} \\ $$$${let}\:{f}\left({z}\right)={z}^{\mathrm{3}} −\mathrm{4}{z}^{\mathrm{2}} +\mathrm{7}{z}−\mathrm{6} \\ $$$$ \\ $$$${finding}\:{the}\:{factor}\:{of}\:{f}\left({z}\right) \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{1}^{\mathrm{3}} −\mathrm{4}\left(\mathrm{1}\right)^{\mathrm{2}} +\mathrm{7}\left(\mathrm{1}\right)−\mathrm{6}=−\mathrm{2}\neq\mathrm{0} \\ $$$$\therefore\:\left({z}−\mathrm{1}\right)\:{is}\:{not}\:{a}\:{factor} \\ $$$${f}\left(\mathrm{2}\right)=\mathrm{2}^{\mathrm{3}} −\mathrm{4}\left(\mathrm{2}\right)^{\mathrm{2}} +\mathrm{7}\left(\mathrm{2}\right)−\mathrm{6}=\mathrm{0} \\ $$$$\therefore\:\left({z}−\mathrm{2}\right)\:{is}\:{a}\:{factor} \\ $$$$ \\ $$$$\frac{{z}^{\mathrm{3}} −\mathrm{4}{z}^{\mathrm{2}} +\mathrm{7}{z}−\mathrm{6}}{{z}−\mathrm{2}}\:/{long}\:{division} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{z}^{\mathrm{2}} −\mathrm{2}{z}+\mathrm{3} \\ $$$${z}−\mathrm{2}\:\sqrt{{z}^{\mathrm{3}} −\mathrm{4}{z}^{\mathrm{2}} +\mathrm{7}{z}−\mathrm{6}} \\ $$$$\frac{−\left({z}^{\mathrm{3}} −\mathrm{2}{z}^{\mathrm{2}} \right)}{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{2}{z}^{\mathrm{2}} +\mathrm{7}{z}} \\ $$$$\frac{\:\:\:\:\:\:−\left(−\mathrm{2}{z}^{\mathrm{2}} +\mathrm{4}{z}\right)}{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}{z}−\mathrm{6}} \\ $$$$\frac{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\left(\mathrm{3}{z}−\mathrm{6}\right)}{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}} \\ $$$${f}\left({z}\right)=\left({z}−\mathrm{2}\right)\left({z}^{\mathrm{2}} −\mathrm{2}{z}+\mathrm{3}\right)=\mathrm{0} \\ $$$${z}−\mathrm{2}=\mathrm{0}\:\:\rightarrow\:\:{z}=\mathrm{2}\:\left({real}\:{root}\right) \\ $$$${z}^{\mathrm{2}} −\mathrm{2}{z}+\mathrm{3}=\mathrm{0} \\ $$$${z}^{\mathrm{2}} −\mathrm{2}{z}+\left(−\mathrm{1}\right)^{\mathrm{2}} =\left(−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{3} \\ $$$$\left({z}−\mathrm{1}\right)^{\mathrm{2}} =−\mathrm{2} \\ $$$${z}−\mathrm{1}=\pm{i}\sqrt{\mathrm{2}},\:\:{i}=\sqrt{−\mathrm{1}} \\ $$$${z}=\mathrm{1}\pm{i}\sqrt{\mathrm{2}} \\ $$$${z}=\mathrm{1}+{i}\sqrt{\mathrm{2}}\:{or}\:{z}=\mathrm{1}−{i}\sqrt{\mathrm{2}}\:\left({complex}\:{root}\right) \\ $$$$ \\ $$$$\therefore\:{the}\:{roots}\:{of}\:{f}\left({z}\right)\:{are}\: \\ $$$${z}=\mathrm{2},\:{z}=\mathrm{1}+{i}\sqrt{\mathrm{2}},\:{z}=\mathrm{1}−{i}\sqrt{\mathrm{2}} \\ $$
