
Question Number 120118 by sarahvalencia last updated on 30/Oct/20
Commented by Dwaipayan Shikari last updated on 29/Oct/20

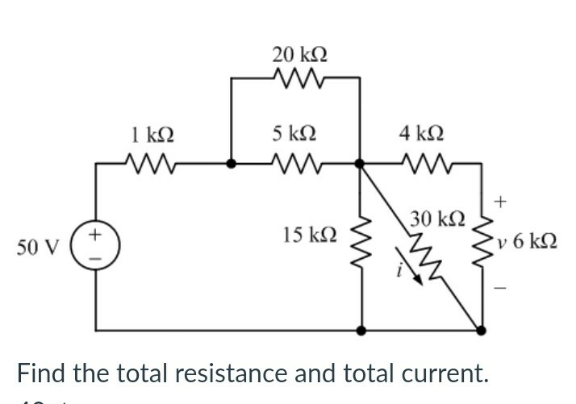
$${Net}\:{resistance}\:\mathrm{10}{k}\Omega \\ $$$${I}=\frac{\mathrm{50}}{\mathrm{10}.\mathrm{10}^{\mathrm{3}} }=\mathrm{5}×\mathrm{10}^{−\mathrm{3}} {A} \\ $$
Commented by Dwaipayan Shikari last updated on 29/Oct/20
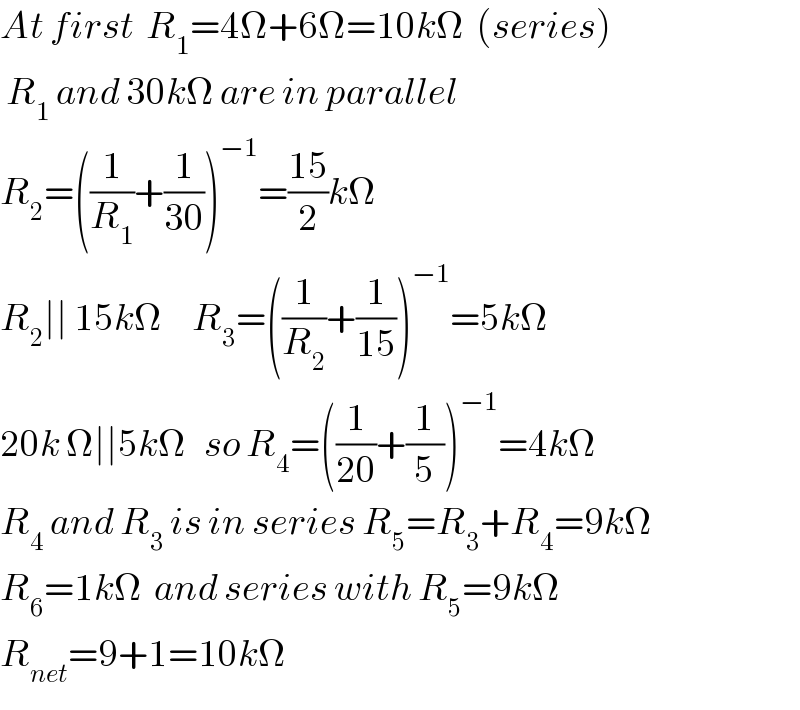
$${At}\:{first}\:\:{R}_{\mathrm{1}} =\mathrm{4}\Omega+\mathrm{6}\Omega=\mathrm{10}{k}\Omega\:\:\left({series}\right) \\ $$$$\:{R}_{\mathrm{1}} \:{and}\:\mathrm{30}{k}\Omega\:{are}\:{in}\:{parallel} \\ $$$${R}_{\mathrm{2}} =\left(\frac{\mathrm{1}}{{R}_{\mathrm{1}} }+\frac{\mathrm{1}}{\mathrm{30}}\right)^{−\mathrm{1}} =\frac{\mathrm{15}}{\mathrm{2}}{k}\Omega \\ $$$${R}_{\mathrm{2}} \mid\mid\:\mathrm{15}{k}\Omega\:\:\:\:\:{R}_{\mathrm{3}} =\left(\frac{\mathrm{1}}{{R}_{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{15}}\right)^{−\mathrm{1}} =\mathrm{5}{k}\Omega \\ $$$$\mathrm{20}{k}\:\Omega\mid\mid\mathrm{5}{k}\Omega\:\:\:{so}\:{R}_{\mathrm{4}} =\left(\frac{\mathrm{1}}{\mathrm{20}}+\frac{\mathrm{1}}{\mathrm{5}}\right)^{−\mathrm{1}} =\mathrm{4}{k}\Omega \\ $$$${R}_{\mathrm{4}} \:{and}\:{R}_{\mathrm{3}} \:{is}\:{in}\:{series}\:{R}_{\mathrm{5}} ={R}_{\mathrm{3}} +{R}_{\mathrm{4}} =\mathrm{9}{k}\Omega \\ $$$${R}_{\mathrm{6}} =\mathrm{1}{k}\Omega\:\:{and}\:{series}\:{with}\:{R}_{\mathrm{5}} =\mathrm{9}{k}\Omega \\ $$$${R}_{{net}} =\mathrm{9}+\mathrm{1}=\mathrm{10}{k}\Omega \\ $$
