
Question Number 11988 by tawa last updated on 08/Apr/17
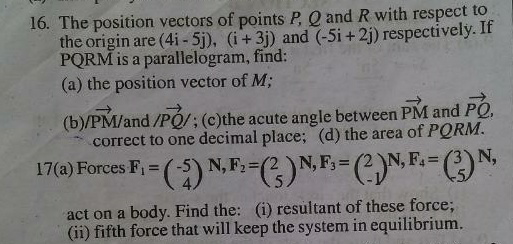
Commented by tawa last updated on 09/Apr/17
$$\mathrm{please}\:\mathrm{help}\:\mathrm{with}\:\mathrm{this}.\:\mathrm{Thanks}\:\mathrm{in}\:\mathrm{advance}.\:\mathrm{16a},\:\mathrm{16b},\:\mathrm{17a} \\ $$
Commented by tawa last updated on 09/Apr/17

$$\mathrm{It}\:\mathrm{remain}\:\mathrm{17a}\:\mathrm{sirs}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{all}\:\mathrm{for}\:\mathrm{the}\:\mathrm{help}. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 09/Apr/17
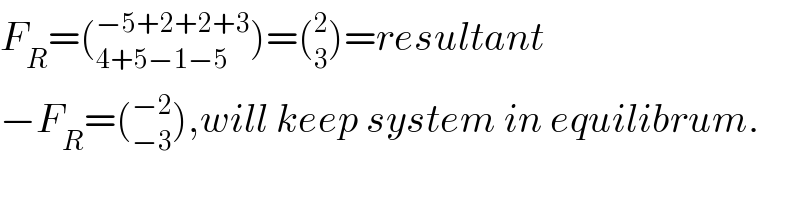
$${F}_{{R}} =\left(_{\mathrm{4}+\mathrm{5}−\mathrm{1}−\mathrm{5}} ^{−\mathrm{5}+\mathrm{2}+\mathrm{2}+\mathrm{3}} \right)=\left(_{\mathrm{3}} ^{\mathrm{2}} \right)={resultant} \\ $$$$−{F}_{{R}} =\left(_{−\mathrm{3}} ^{−\mathrm{2}} \right),{will}\:{keep}\:{system}\:{in}\:{equilibrum}. \\ $$
Answered by ajfour last updated on 09/Apr/17
Commented by ajfour last updated on 09/Apr/17
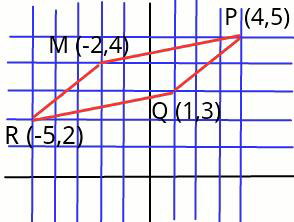
![let OM= xi^� +yj^� RM=QP ⇒ (x+5)i^� +(y−2)j^� =3i^� +2j^� so, x= −2 and y =4 . ∣PM∣=(√([4−(−2)]^2 +(5−4)^2 )) =(√(37)) ∣PQ∣=(√((4−1)^2 +(5−3)^2 )) =(√(13)) cos θ =((QP.MP)/(∣QP∣∣MP∣)) = (([(4−1)i^� +(5−3)j^� ].[(4−(−2))i^� +(5−4)j^� ])/((√(3^2 +2^2 )) (√(6^2 +1^2 )))) cos θ =((20)/((√(13))(√(37)))) Area PQRM =QP×MP = (3i^� +2j^� )×(6i^� +j^� ) = 18k^� −12k^� = 6k^� .](Q11993.png)
$${let}\:\boldsymbol{{OM}}=\:{x}\hat {{i}}+{y}\hat {{j}} \\ $$$$\boldsymbol{{RM}}=\boldsymbol{{QP}}\: \\ $$$$\Rightarrow\:\left({x}+\mathrm{5}\right)\hat {{i}}+\left({y}−\mathrm{2}\right)\hat {{j}}\:=\mathrm{3}\hat {{i}}+\mathrm{2}\hat {{j}} \\ $$$${so},\:{x}=\:−\mathrm{2}\:\:{and}\:\:{y}\:=\mathrm{4}\:\:. \\ $$$$\mid\boldsymbol{{PM}}\mid=\sqrt{\left[\mathrm{4}−\left(−\mathrm{2}\right)\right]^{\mathrm{2}} +\left(\mathrm{5}−\mathrm{4}\right)^{\mathrm{2}} }\:=\sqrt{\mathrm{37}} \\ $$$$\mid\boldsymbol{{PQ}}\mid=\sqrt{\left(\mathrm{4}−\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{5}−\mathrm{3}\right)^{\mathrm{2}} }\:=\sqrt{\mathrm{13}} \\ $$$$\mathrm{cos}\:\theta\:=\frac{\boldsymbol{{QP}}.\boldsymbol{{MP}}}{\mid\boldsymbol{{QP}}\mid\mid\boldsymbol{{MP}}\mid} \\ $$$$\:\:\:=\:\frac{\left[\left(\mathrm{4}−\mathrm{1}\right)\hat {{i}}+\left(\mathrm{5}−\mathrm{3}\right)\hat {{j}}\right].\left[\left(\mathrm{4}−\left(−\mathrm{2}\right)\right)\hat {{i}}+\left(\mathrm{5}−\mathrm{4}\right)\hat {{j}}\right]}{\sqrt{\mathrm{3}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }\:\sqrt{\mathrm{6}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} }} \\ $$$$\:\:\:\mathrm{cos}\:\theta\:=\frac{\mathrm{20}}{\sqrt{\mathrm{13}}\sqrt{\mathrm{37}}} \\ $$$${Area}\:{PQRM}\:=\boldsymbol{{QP}}×\boldsymbol{{MP}} \\ $$$$\:\:\:\:\:\:\:\:=\:\left(\mathrm{3}\hat {{i}}+\mathrm{2}\hat {{j}}\right)×\left(\mathrm{6}\hat {{i}}+\hat {{j}}\right) \\ $$$$\:\:\:\:\:\:\:\:=\:\mathrm{18}\hat {{k}}−\mathrm{12}\hat {{k}}\:=\:\mathrm{6}\hat {{k}}\:. \\ $$$$ \\ $$$$\:\:\:\:\: \\ $$
Commented by tawa last updated on 09/Apr/17
$$\mathrm{Wow},\:\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by tawa last updated on 09/Apr/17
$$\mathrm{Please}\:\mathrm{sir}.\:\mathrm{it}\:\mathrm{remain}\:\mathrm{number}\:\mathrm{17a} \\ $$
Answered by mrW1 last updated on 09/Apr/17
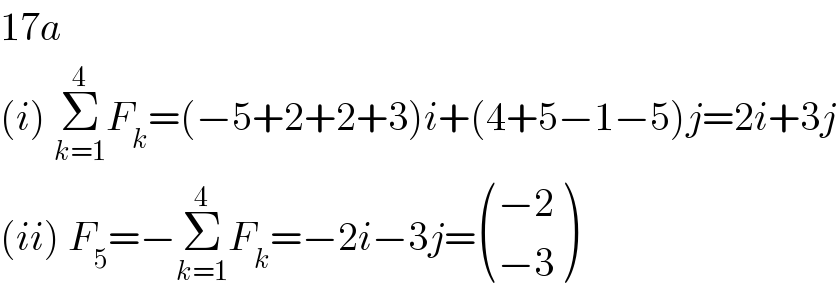
$$\mathrm{17}{a} \\ $$$$\left({i}\right)\:\underset{{k}=\mathrm{1}} {\overset{\mathrm{4}} {\sum}}{F}_{{k}} =\left(−\mathrm{5}+\mathrm{2}+\mathrm{2}+\mathrm{3}\right){i}+\left(\mathrm{4}+\mathrm{5}−\mathrm{1}−\mathrm{5}\right){j}=\mathrm{2}{i}+\mathrm{3}{j} \\ $$$$\left({ii}\right)\:{F}_{\mathrm{5}} =−\underset{{k}=\mathrm{1}} {\overset{\mathrm{4}} {\sum}}{F}_{{k}} =−\mathrm{2}{i}−\mathrm{3}{j}=\begin{pmatrix}{−\mathrm{2}}\\{−\mathrm{3}}\end{pmatrix} \\ $$
Commented by tawa last updated on 09/Apr/17

$$\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\: \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 09/Apr/17
$${hi}\:{mrW}\mathrm{1}.{please}\:{see}\:{Q}.{n}:\mathrm{11338}. \\ $$
Commented by mrW1 last updated on 10/Apr/17
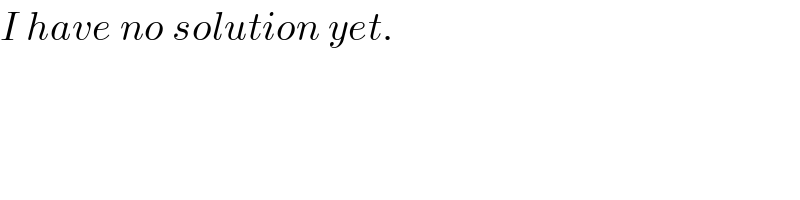
$${I}\:{have}\:{no}\:{solution}\:{yet}. \\ $$
