
Question Number 119160 by zakirullah last updated on 22/Oct/20
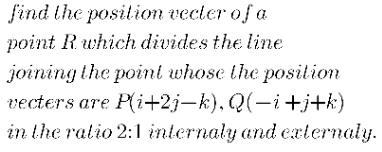
Commented by zakirullah last updated on 22/Oct/20

$$\boldsymbol{\mathrm{find}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{position}}\:\boldsymbol{\mathrm{vecter}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{a}}\:\boldsymbol{{p}\mathrm{oint}}\:\boldsymbol{\mathrm{R}} \\ $$$$\boldsymbol{{which}}\:\boldsymbol{{divides}}\:\boldsymbol{{the}}\:\boldsymbol{{line}}\:\boldsymbol{{joining}} \\ $$$$\boldsymbol{{the}}\:\boldsymbol{{point}}\:\boldsymbol{{whose}}\:\boldsymbol{{the}}\:\boldsymbol{{position}} \\ $$$$\boldsymbol{{vecters}}\:\boldsymbol{{are}}\:\boldsymbol{{P}}\left(\boldsymbol{{i}}+\mathrm{2}\boldsymbol{{j}}−\boldsymbol{{k}}\right),\boldsymbol{{Q}}\left(−\boldsymbol{{i}}+\boldsymbol{{j}}+\boldsymbol{{k}}\right)\:\boldsymbol{{in}} \\ $$$$\boldsymbol{{the}}\:\boldsymbol{{ratio}}\:\mathrm{2}:\mathrm{1}\:\boldsymbol{{internaly}}\:\boldsymbol{{and}}\:\boldsymbol{{externaly}} \\ $$
Commented by zakirullah last updated on 22/Oct/20
$$\boldsymbol{{Please}}\:\boldsymbol{{help}}??\upuparrows \\ $$
Commented by PRITHWISH SEN 2 last updated on 22/Oct/20
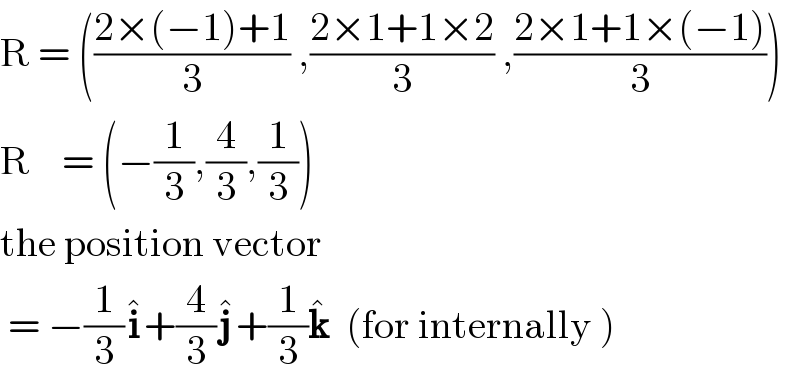
$$\mathrm{R}\:=\:\left(\frac{\mathrm{2}×\left(−\mathrm{1}\right)+\mathrm{1}}{\mathrm{3}}\:,\frac{\mathrm{2}×\mathrm{1}+\mathrm{1}×\mathrm{2}}{\mathrm{3}}\:,\frac{\mathrm{2}×\mathrm{1}+\mathrm{1}×\left(−\mathrm{1}\right)}{\mathrm{3}}\right) \\ $$$$\mathrm{R}\:\:\:\:=\:\left(−\frac{\mathrm{1}}{\mathrm{3}},\frac{\mathrm{4}}{\mathrm{3}},\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$\mathrm{the}\:\mathrm{position}\:\mathrm{vector} \\ $$$$\:=\:−\frac{\mathrm{1}}{\mathrm{3}}\hat {\boldsymbol{\mathrm{i}}}+\frac{\mathrm{4}}{\mathrm{3}}\hat {\boldsymbol{\mathrm{j}}}+\frac{\mathrm{1}}{\mathrm{3}}\hat {\boldsymbol{\mathrm{k}}}\:\:\left(\mathrm{for}\:\mathrm{internally}\:\right) \\ $$
Commented by zakirullah last updated on 22/Oct/20
$$\boldsymbol{{sorry}}\:\boldsymbol{{sir}}\:\boldsymbol{{i}}\:\boldsymbol{{think}}\:\boldsymbol{{this}}\:\boldsymbol{{mathod}}\:\boldsymbol{{is}} \\ $$$$\boldsymbol{{very}}\:\boldsymbol{{high}} \\ $$$$\boldsymbol{{please}}\:\boldsymbol{{can}}\:\boldsymbol{{you}}\:\boldsymbol{{explain}}\:\boldsymbol{{it}}\:\boldsymbol{{in}}\:\boldsymbol{{another}}\:\boldsymbol{{way}}? \\ $$
Commented by PRITHWISH SEN 2 last updated on 22/Oct/20

$$\mathrm{think}\:\mathrm{P}\:\mathrm{and}\:\mathrm{Q}\:\mathrm{as}\:\mathrm{points}\:\mathrm{in}\:\mathrm{3D} \\ $$$$\mathrm{then}\:\mathrm{P}=\left(\mathrm{1},\mathrm{2},−\mathrm{1}\right)\:\&\:\mathrm{Q}=\left(−\mathrm{1},\mathrm{1},\mathrm{1}\right) \\ $$$$\mathrm{and}\:\mathrm{find}\:\mathrm{R}\:\mathrm{as}\:\mathrm{internally}\:\mathrm{divides}\:\mathrm{PQ}\:\mathrm{in}\:\mathrm{the}\: \\ $$$$\mathrm{ratio}\:\mathrm{2}:\mathrm{1}\:\mathrm{by}\:\mathrm{the}\:\mathrm{use}\:\mathrm{of}\:\mathrm{section}\:\mathrm{fomula}. \\ $$$$\mathrm{then}\:\mathrm{just}\:\mathrm{put}\:\mathrm{it}\:\mathrm{with}\:\boldsymbol{\mathrm{i}},\boldsymbol{\mathrm{j}},\boldsymbol{\mathrm{k}}. \\ $$
