
Question Number 119155 by zakirullah last updated on 22/Oct/20
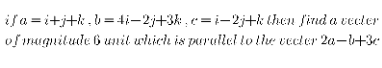
Commented by zakirullah last updated on 22/Oct/20
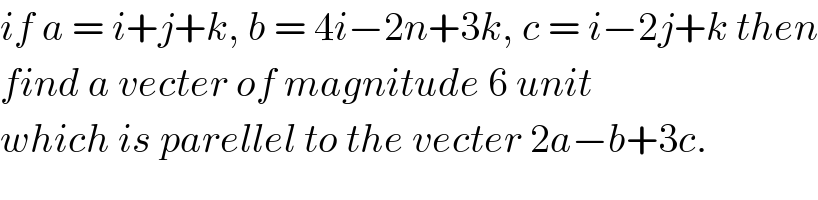
$${if}\:{a}\:=\:{i}+{j}+{k},\:{b}\:=\:\mathrm{4}{i}−\mathrm{2}{n}+\mathrm{3}{k},\:{c}\:=\:{i}−\mathrm{2}{j}+{k}\:{then} \\ $$$${find}\:{a}\:{vecter}\:{of}\:{magnitude}\:\mathrm{6}\:{unit} \\ $$$${which}\:{is}\:{parellel}\:{to}\:{the}\:{vecter}\:\mathrm{2}{a}−{b}+\mathrm{3}{c}. \\ $$
Commented by PRITHWISH SEN 2 last updated on 22/Oct/20

$$\mathrm{2a}−\mathrm{b}+\mathrm{3c}=\left(\mathrm{2}−\mathrm{4}+\mathrm{3}\right)\mathrm{i}+\left(\mathrm{2}+\mathrm{2}−\mathrm{6}\right)\mathrm{j}+\left(\mathrm{2}−\mathrm{3}+\mathrm{3}\right)\mathrm{k} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{i}−\mathrm{2j}+\mathrm{2k}...\left(\mathrm{i}\right) \\ $$$$\mathrm{let}\:\mathrm{the}\:\mathrm{parallel}\:\mathrm{vecor}\:\mathrm{to}\:\left(\mathrm{i}\right)\:\mathrm{is} \\ $$$$\mathrm{p}\boldsymbol{\mathrm{i}}+\mathrm{q}\boldsymbol{\mathrm{j}}+\mathrm{r}\boldsymbol{\mathrm{k}} \\ $$$$\therefore\frac{\mathrm{p}}{\mathrm{1}}=\frac{\mathrm{q}}{−\mathrm{2}}=\frac{\mathrm{r}}{\mathrm{2}}\:=\:\lambda\:\mathrm{say} \\ $$$$\mathrm{now}\:\mathrm{p}^{\mathrm{2}} +\mathrm{q}^{\mathrm{2}} +\mathrm{r}^{\mathrm{2}} =\:\mathrm{6}^{\mathrm{2}} =\:\mathrm{36} \\ $$$$\lambda^{\mathrm{2}} \left(\mathrm{1}+\mathrm{4}+\mathrm{4}\right)=\mathrm{36}\Rightarrow\lambda=\pm\mathrm{2} \\ $$$$\mathrm{the}\:\mathrm{required}\:\mathrm{vector} \\ $$$$\mathrm{2i}−\mathrm{4j}+\mathrm{4k} \\ $$$$\:\:\:\:\mathrm{or} \\ $$$$−\mathrm{2i}+\mathrm{4j}−\mathrm{4k} \\ $$$$\mathrm{sorry}\:\mathrm{i}\:\mathrm{have}\:\mathrm{fix}\:\mathrm{it}.\mathrm{i}\:\mathrm{am}\:\mathrm{making}\:\mathrm{typo}\:\mathrm{a}\:\mathrm{habbit}. \\ $$
Commented by zakirullah last updated on 22/Oct/20
$$\boldsymbol{{Sir}}\:\boldsymbol{{a}}\:\boldsymbol{{boundle}}\:\boldsymbol{{of}}\:\boldsymbol{{thanks}} \\ $$
Commented by PRITHWISH SEN 2 last updated on 22/Oct/20

$$\mathrm{welcome} \\ $$
Commented by zakirullah last updated on 22/Oct/20
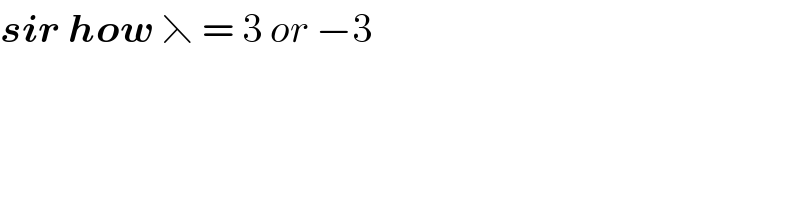
$$\boldsymbol{{sir}}\:\boldsymbol{{how}}\:\leftthreetimes\:=\:\mathrm{3}\:{or}\:−\mathrm{3} \\ $$
Answered by Dwaipayan Shikari last updated on 22/Oct/20
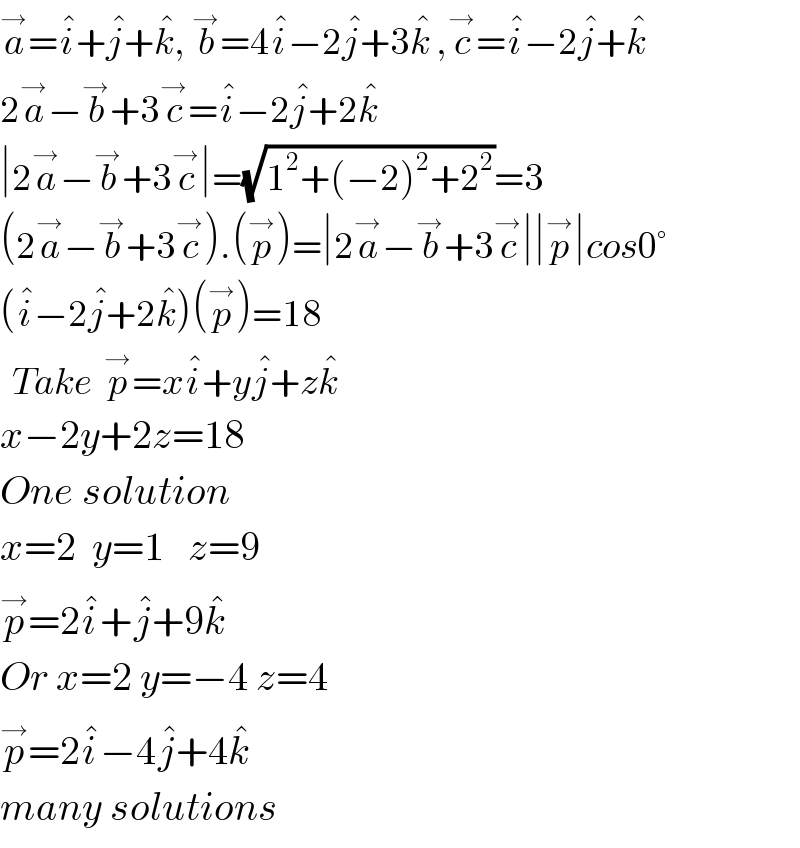
$$\overset{\rightarrow} {{a}}=\hat {{i}}+\hat {{j}}+\hat {{k}},\:\overset{\rightarrow} {{b}}=\mathrm{4}\hat {{i}}−\mathrm{2}\hat {{j}}+\mathrm{3}\hat {{k}}\:,\overset{\rightarrow} {{c}}=\hat {{i}}−\mathrm{2}\hat {{j}}+\hat {{k}} \\ $$$$\mathrm{2}\overset{\rightarrow} {{a}}−\overset{\rightarrow} {{b}}+\mathrm{3}\overset{\rightarrow} {{c}}=\hat {{i}}−\mathrm{2}\hat {{j}}+\mathrm{2}\hat {{k}} \\ $$$$\mid\mathrm{2}\overset{\rightarrow} {{a}}−\overset{\rightarrow} {{b}}+\mathrm{3}\overset{\rightarrow} {{c}}\mid=\sqrt{\mathrm{1}^{\mathrm{2}} +\left(−\mathrm{2}\right)^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }=\mathrm{3} \\ $$$$\left(\mathrm{2}\overset{\rightarrow} {{a}}−\overset{\rightarrow} {{b}}+\mathrm{3}\overset{\rightarrow} {{c}}\right).\left(\overset{\rightarrow} {{p}}\right)=\mid\mathrm{2}\overset{\rightarrow} {{a}}−\overset{\rightarrow} {{b}}+\mathrm{3}\overset{\rightarrow} {{c}}\mid\mid\overset{\rightarrow} {{p}}\mid{cos}\mathrm{0}° \\ $$$$\left(\hat {{i}}−\mathrm{2}\hat {{j}}+\mathrm{2}\hat {{k}}\right)\left(\overset{\rightarrow} {{p}}\right)=\mathrm{18} \\ $$$$\:\:{Take}\:\:\overset{\rightarrow} {{p}}={x}\hat {{i}}+{y}\hat {{j}}+{z}\hat {{k}}\:\: \\ $$$${x}−\mathrm{2}{y}+\mathrm{2}{z}=\mathrm{18} \\ $$$${One}\:{solution} \\ $$$${x}=\mathrm{2}\:\:{y}=\mathrm{1}\:\:\:{z}=\mathrm{9} \\ $$$$\overset{\rightarrow} {{p}}=\mathrm{2}\hat {{i}}+\hat {{j}}+\mathrm{9}\hat {{k}} \\ $$$${Or}\:{x}=\mathrm{2}\:{y}=−\mathrm{4}\:{z}=\mathrm{4} \\ $$$$\overset{\rightarrow} {{p}}=\mathrm{2}\hat {{i}}−\mathrm{4}\hat {{j}}+\mathrm{4}\hat {{k}} \\ $$$${many}\:{solutions} \\ $$
