Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 119119 by benjo_mathlover last updated on 22/Oct/20

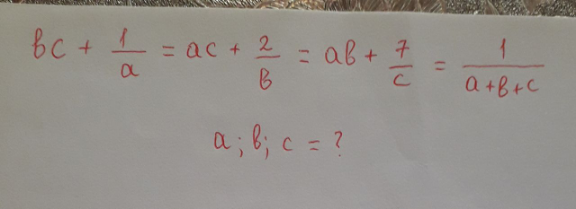
Answered by mindispower last updated on 22/Oct/20

⇒abc+1=(a/(a+b+c))...1 abc+2=(b/(a+b+c))....2 abc+7=(c/(a+b+c))...3 abc+10=1 ⇒abc=−9...2 ⇒bc=−(9/a),ac=((−9)/b) bc+(1/a)=−(8/a)=−(7/b)=−(2/c) b=((8a)/7),c=(a/4) 2⇔((8a^3 )/(28))=−9⇒a^3 =((−63)/4) a=−(((63)/4))^(1/3) ,real solution ,z=(√((63)/4))e^((2iπ)/3) ,z^−

$$\Rightarrow{abc}+\mathrm{1}=\frac{{a}}{{a}+{b}+{c}}...\mathrm{1} \\ $$$${abc}+\mathrm{2}=\frac{{b}}{{a}+{b}+{c}}....\mathrm{2} \\ $$$${abc}+\mathrm{7}=\frac{{c}}{{a}+{b}+{c}}...\mathrm{3} \\ $$$${abc}+\mathrm{10}=\mathrm{1} \\ $$$$\Rightarrow{abc}=−\mathrm{9}...\mathrm{2} \\ $$$$\Rightarrow{bc}=−\frac{\mathrm{9}}{{a}},{ac}=\frac{−\mathrm{9}}{{b}} \\ $$$${bc}+\frac{\mathrm{1}}{{a}}=−\frac{\mathrm{8}}{{a}}=−\frac{\mathrm{7}}{{b}}=−\frac{\mathrm{2}}{{c}} \\ $$$${b}=\frac{\mathrm{8}{a}}{\mathrm{7}},{c}=\frac{{a}}{\mathrm{4}} \\ $$$$\mathrm{2}\Leftrightarrow\frac{\mathrm{8}{a}^{\mathrm{3}} }{\mathrm{28}}=−\mathrm{9}\Rightarrow{a}^{\mathrm{3}} =\frac{−\mathrm{63}}{\mathrm{4}} \\ $$$${a}=−\sqrt[{\mathrm{3}}]{\frac{\mathrm{63}}{\mathrm{4}}},{real}\:{solution}\:,{z}=\sqrt{\frac{\mathrm{63}}{\mathrm{4}}}{e}^{\frac{\mathrm{2}{i}\pi}{\mathrm{3}}} ,\overset{−} {{z}} \\ $$$$ \\ $$

Answered by bemath last updated on 22/Oct/20

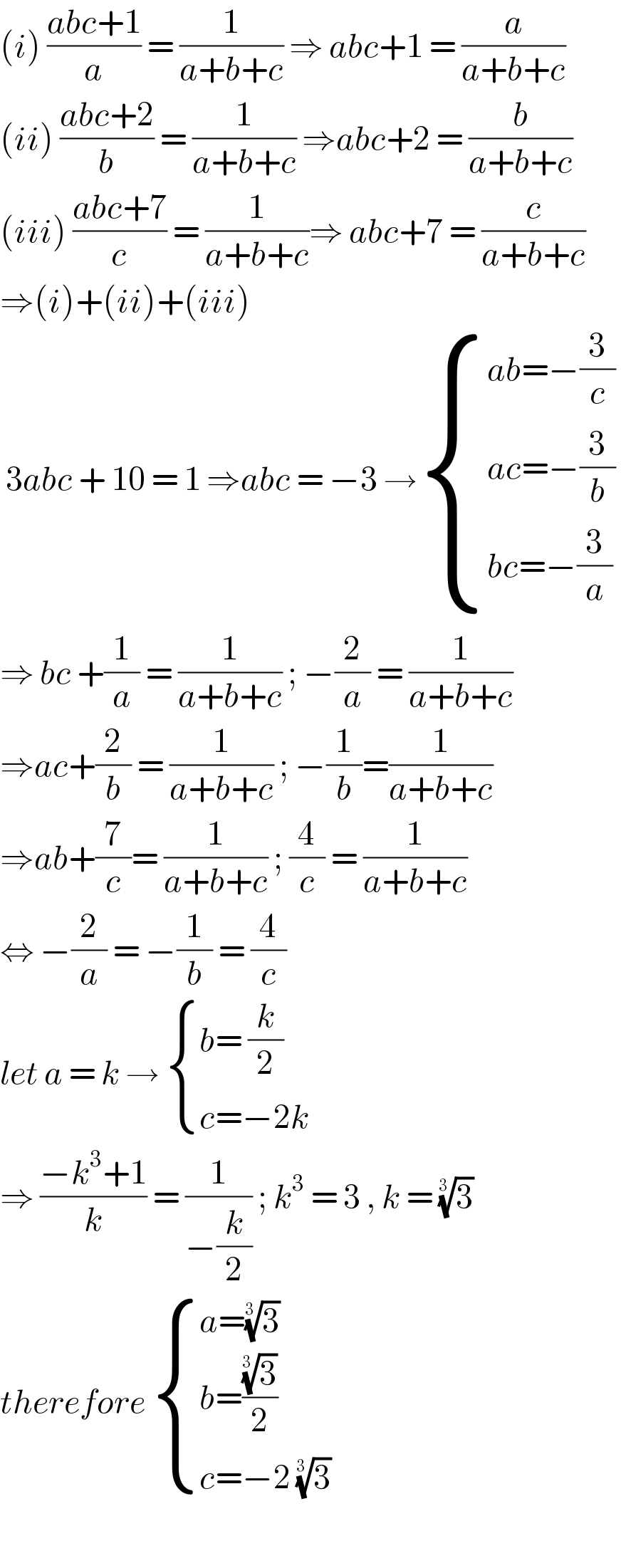
(i) ((abc+1)/a) = (1/(a+b+c)) ⇒ abc+1 = (a/(a+b+c)) (ii) ((abc+2)/b) = (1/(a+b+c)) ⇒abc+2 = (b/(a+b+c)) (iii) ((abc+7)/c) = (1/(a+b+c))⇒ abc+7 = (c/(a+b+c)) ⇒(i)+(ii)+(iii) 3abc + 10 = 1 ⇒abc = −3 → { ((ab=−(3/c))),((ac=−(3/b) )),((bc=−(3/a))) :} ⇒ bc +(1/a) = (1/(a+b+c)) ; −(2/a) = (1/(a+b+c)) ⇒ac+(2/b) = (1/(a+b+c)) ; −(1/b)=(1/(a+b+c)) ⇒ab+(7/c)= (1/(a+b+c)) ; (4/c) = (1/(a+b+c)) ⇔ −(2/a) = −(1/b) = (4/c) let a = k → { ((b= (k/2))),((c=−2k)) :} ⇒ ((−k^3 +1)/k) = (1/(−(k/2))) ; k^3 = 3 , k = (3)^(1/(3 )) therefore { ((a=(3)^(1/(3 )) )),((b=((3)^(1/(3 )) /2) )),((c=−2 (3)^(1/(3 )) )) :}

$$\left({i}\right)\:\frac{{abc}+\mathrm{1}}{{a}}\:=\:\frac{\mathrm{1}}{{a}+{b}+{c}}\:\Rightarrow\:{abc}+\mathrm{1}\:=\:\frac{{a}}{{a}+{b}+{c}} \\ $$$$\left({ii}\right)\:\frac{{abc}+\mathrm{2}}{{b}}\:=\:\frac{\mathrm{1}}{{a}+{b}+{c}}\:\Rightarrow{abc}+\mathrm{2}\:=\:\frac{{b}}{{a}+{b}+{c}} \\ $$$$\left({iii}\right)\:\frac{{abc}+\mathrm{7}}{{c}}\:=\:\frac{\mathrm{1}}{{a}+{b}+{c}}\Rightarrow\:{abc}+\mathrm{7}\:=\:\frac{{c}}{{a}+{b}+{c}} \\ $$$$\Rightarrow\left({i}\right)+\left({ii}\right)+\left({iii}\right) \\ $$$$\:\mathrm{3}{abc}\:+\:\mathrm{10}\:=\:\mathrm{1}\:\Rightarrow{abc}\:=\:−\mathrm{3}\:\rightarrow\begin{cases}{{ab}=−\frac{\mathrm{3}}{{c}}}\\{{ac}=−\frac{\mathrm{3}}{{b}}\:}\\{{bc}=−\frac{\mathrm{3}}{{a}}}\end{cases} \\ $$$$\Rightarrow\:{bc}\:+\frac{\mathrm{1}}{{a}}\:=\:\frac{\mathrm{1}}{{a}+{b}+{c}}\:;\:−\frac{\mathrm{2}}{{a}}\:=\:\frac{\mathrm{1}}{{a}+{b}+{c}} \\ $$$$\Rightarrow{ac}+\frac{\mathrm{2}}{{b}}\:=\:\frac{\mathrm{1}}{{a}+{b}+{c}}\:;\:−\frac{\mathrm{1}}{{b}}=\frac{\mathrm{1}}{{a}+{b}+{c}} \\ $$$$\Rightarrow{ab}+\frac{\mathrm{7}}{{c}}=\:\frac{\mathrm{1}}{{a}+{b}+{c}}\:;\:\frac{\mathrm{4}}{{c}}\:=\:\frac{\mathrm{1}}{{a}+{b}+{c}} \\ $$$$\Leftrightarrow\:−\frac{\mathrm{2}}{{a}}\:=\:−\frac{\mathrm{1}}{{b}}\:=\:\frac{\mathrm{4}}{{c}}\: \\ $$$${let}\:{a}\:=\:{k}\:\rightarrow\:\begin{cases}{{b}=\:\frac{{k}}{\mathrm{2}}}\\{{c}=−\mathrm{2}{k}}\end{cases} \\ $$$$\Rightarrow\:\frac{−{k}^{\mathrm{3}} +\mathrm{1}}{{k}}\:=\:\frac{\mathrm{1}}{−\frac{{k}}{\mathrm{2}}}\:;\:{k}^{\mathrm{3}} \:=\:\mathrm{3}\:,\:{k}\:=\:\sqrt[{\mathrm{3}\:}]{\mathrm{3}} \\ $$$${therefore}\:\begin{cases}{{a}=\sqrt[{\mathrm{3}\:}]{\mathrm{3}}}\\{{b}=\frac{\sqrt[{\mathrm{3}\:}]{\mathrm{3}}}{\mathrm{2}}\:}\\{{c}=−\mathrm{2}\:\sqrt[{\mathrm{3}\:}]{\mathrm{3}}}\end{cases} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com