
Question Number 118791 by Algoritm last updated on 19/Oct/20
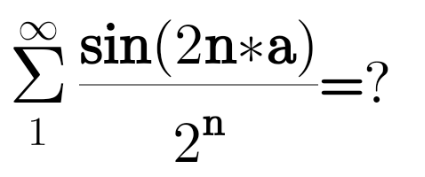
Answered by Olaf last updated on 19/Oct/20
![f_p (a) = Σ_(n=1) ^p ((sin(2n∗a))/2^n ) f_p (a) = Σ_(n=1) ^p ((e^(i2na) −e^(−i2na) )/(2^(n+1) i)) f_p (a) = (1/(2i))Σ_(n=1) ^p ((e^(2ia) /2))^n −(1/(2i))Σ_(n=1) ^p ((e^(−2ia) /2))^n f_p (a) = (1/(2i)).(e^(2ia) /2).((1−(e^(2iap) /2^p ))/(1−(e^(2ia) /2)))−(1/(2i)).(e^(−2ia) /2).((1−(e^(−2iap) /2^p ))/(1−(e^(−2ia) /2))) f_∞ (a) = (1/(2i)).(e^(2ia) /2).(1/(1−(e^(2ia) /2)))−(1/(2i)).(e^(−2ia) /2).(1/(1−(e^(−2ia) /2))) f_∞ (a) = (1/(2i)).(e^(2ia) /(2−e^(2ia) ))−(1/(2i)).(e^(−2ia) /(2−e^(−2ia) )) f_∞ (a) = (1/(2i))[(e^(2ia) /(2−e^(2ia) ))−(e^(−2ia) /(2−e^(−2ia) ))] f_∞ (a) = (1/(2i))[((e^(2ia) (2−e^(−2ia) )−e^(−2ia) (2−e^(2ia) ))/((2−e^(2ia) )(2−e^(−2ia) )))] f_∞ (a) = (1/(2i))[((2(e^(2ia) −e^(−2ia) ))/(4−2(e^(2ia) +e^(−2ia) )+1))] f_∞ (a) = ((2sin(2a))/(5−4cos(2a)))](Q118801.png)
$${f}_{{p}} \left({a}\right)\:=\:\underset{{n}=\mathrm{1}} {\overset{{p}} {\sum}}\frac{\mathrm{sin}\left(\mathrm{2}{n}\ast{a}\right)}{\mathrm{2}^{{n}} } \\ $$$${f}_{{p}} \left({a}\right)\:=\:\underset{{n}=\mathrm{1}} {\overset{{p}} {\sum}}\frac{{e}^{{i}\mathrm{2}{na}} −{e}^{−{i}\mathrm{2}{na}} }{\mathrm{2}^{{n}+\mathrm{1}} {i}} \\ $$$${f}_{{p}} \left({a}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}{i}}\underset{{n}=\mathrm{1}} {\overset{{p}} {\sum}}\left(\frac{{e}^{\mathrm{2}{ia}} }{\mathrm{2}}\right)^{{n}} −\frac{\mathrm{1}}{\mathrm{2}{i}}\underset{{n}=\mathrm{1}} {\overset{{p}} {\sum}}\left(\frac{{e}^{−\mathrm{2}{ia}} }{\mathrm{2}}\right)^{{n}} \\ $$$${f}_{{p}} \left({a}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}{i}}.\frac{{e}^{\mathrm{2}{ia}} }{\mathrm{2}}.\frac{\mathrm{1}−\frac{{e}^{\mathrm{2}{iap}} }{\mathrm{2}^{{p}} }}{\mathrm{1}−\frac{{e}^{\mathrm{2}{ia}} }{\mathrm{2}}}−\frac{\mathrm{1}}{\mathrm{2}{i}}.\frac{{e}^{−\mathrm{2}{ia}} }{\mathrm{2}}.\frac{\mathrm{1}−\frac{{e}^{−\mathrm{2}{iap}} }{\mathrm{2}^{{p}} }}{\mathrm{1}−\frac{{e}^{−\mathrm{2}{ia}} }{\mathrm{2}}} \\ $$$${f}_{\infty} \left({a}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}{i}}.\frac{{e}^{\mathrm{2}{ia}} }{\mathrm{2}}.\frac{\mathrm{1}}{\mathrm{1}−\frac{{e}^{\mathrm{2}{ia}} }{\mathrm{2}}}−\frac{\mathrm{1}}{\mathrm{2}{i}}.\frac{{e}^{−\mathrm{2}{ia}} }{\mathrm{2}}.\frac{\mathrm{1}}{\mathrm{1}−\frac{{e}^{−\mathrm{2}{ia}} }{\mathrm{2}}} \\ $$$${f}_{\infty} \left({a}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}{i}}.\frac{{e}^{\mathrm{2}{ia}} }{\mathrm{2}−{e}^{\mathrm{2}{ia}} }−\frac{\mathrm{1}}{\mathrm{2}{i}}.\frac{{e}^{−\mathrm{2}{ia}} }{\mathrm{2}−{e}^{−\mathrm{2}{ia}} } \\ $$$${f}_{\infty} \left({a}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}{i}}\left[\frac{{e}^{\mathrm{2}{ia}} }{\mathrm{2}−{e}^{\mathrm{2}{ia}} }−\frac{{e}^{−\mathrm{2}{ia}} }{\mathrm{2}−{e}^{−\mathrm{2}{ia}} }\right] \\ $$$${f}_{\infty} \left({a}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}{i}}\left[\frac{{e}^{\mathrm{2}{ia}} \left(\mathrm{2}−{e}^{−\mathrm{2}{ia}} \right)−{e}^{−\mathrm{2}{ia}} \left(\mathrm{2}−{e}^{\mathrm{2}{ia}} \right)}{\left(\mathrm{2}−{e}^{\mathrm{2}{ia}} \right)\left(\mathrm{2}−{e}^{−\mathrm{2}{ia}} \right)}\right] \\ $$$${f}_{\infty} \left({a}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}{i}}\left[\frac{\mathrm{2}\left({e}^{\mathrm{2}{ia}} −{e}^{−\mathrm{2}{ia}} \right)}{\mathrm{4}−\mathrm{2}\left({e}^{\mathrm{2}{ia}} +{e}^{−\mathrm{2}{ia}} \right)+\mathrm{1}}\right] \\ $$$${f}_{\infty} \left({a}\right)\:=\:\frac{\mathrm{2sin}\left(\mathrm{2}{a}\right)}{\mathrm{5}−\mathrm{4cos}\left(\mathrm{2}{a}\right)} \\ $$
Answered by mathmax by abdo last updated on 19/Oct/20
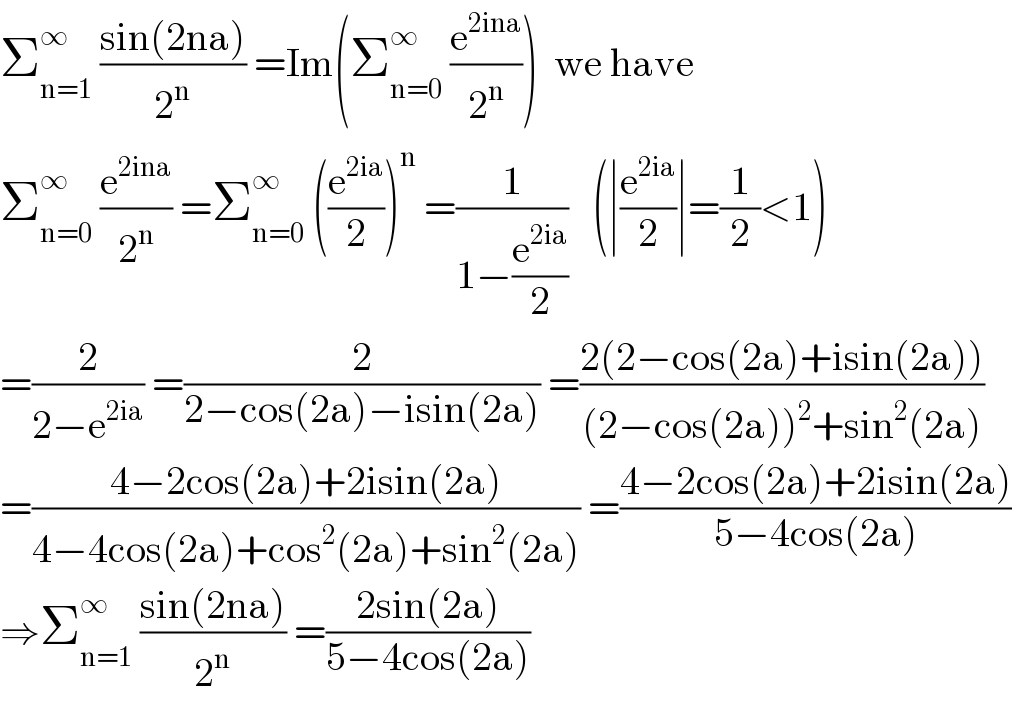
$$\sum_{\mathrm{n}=\mathrm{1}} ^{\infty\:} \:\frac{\mathrm{sin}\left(\mathrm{2na}\right)}{\mathrm{2}^{\mathrm{n}} }\:=\mathrm{Im}\left(\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{\mathrm{2ina}} }{\mathrm{2}^{\mathrm{n}} }\right)\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{\mathrm{2ina}} }{\mathrm{2}^{\mathrm{n}} }\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(\frac{\mathrm{e}^{\mathrm{2ia}} }{\mathrm{2}}\right)^{\mathrm{n}} \:=\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{e}^{\mathrm{2ia}} }{\mathrm{2}}}\:\:\:\left(\mid\frac{\mathrm{e}^{\mathrm{2ia}} }{\mathrm{2}}\mid=\frac{\mathrm{1}}{\mathrm{2}}<\mathrm{1}\right) \\ $$$$=\frac{\mathrm{2}}{\mathrm{2}−\mathrm{e}^{\mathrm{2ia}} }\:=\frac{\mathrm{2}}{\mathrm{2}−\mathrm{cos}\left(\mathrm{2a}\right)−\mathrm{isin}\left(\mathrm{2a}\right)}\:=\frac{\mathrm{2}\left(\mathrm{2}−\mathrm{cos}\left(\mathrm{2a}\right)+\mathrm{isin}\left(\mathrm{2a}\right)\right)}{\left(\mathrm{2}−\mathrm{cos}\left(\mathrm{2a}\right)\right)^{\mathrm{2}} +\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2a}\right)} \\ $$$$=\frac{\mathrm{4}−\mathrm{2cos}\left(\mathrm{2a}\right)+\mathrm{2isin}\left(\mathrm{2a}\right)}{\mathrm{4}−\mathrm{4cos}\left(\mathrm{2a}\right)+\mathrm{cos}^{\mathrm{2}} \left(\mathrm{2a}\right)+\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2a}\right)}\:=\frac{\mathrm{4}−\mathrm{2cos}\left(\mathrm{2a}\right)+\mathrm{2isin}\left(\mathrm{2a}\right)}{\mathrm{5}−\mathrm{4cos}\left(\mathrm{2a}\right)} \\ $$$$\Rightarrow\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{sin}\left(\mathrm{2na}\right)}{\mathrm{2}^{\mathrm{n}} }\:=\frac{\mathrm{2sin}\left(\mathrm{2a}\right)}{\mathrm{5}−\mathrm{4cos}\left(\mathrm{2a}\right)} \\ $$
