
Question Number 118083 by pramod1977 last updated on 15/Oct/20
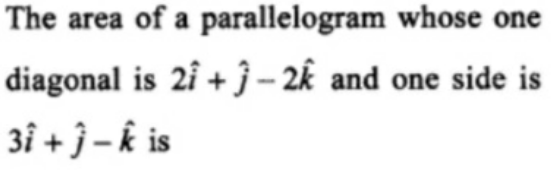
Answered by bemath last updated on 15/Oct/20
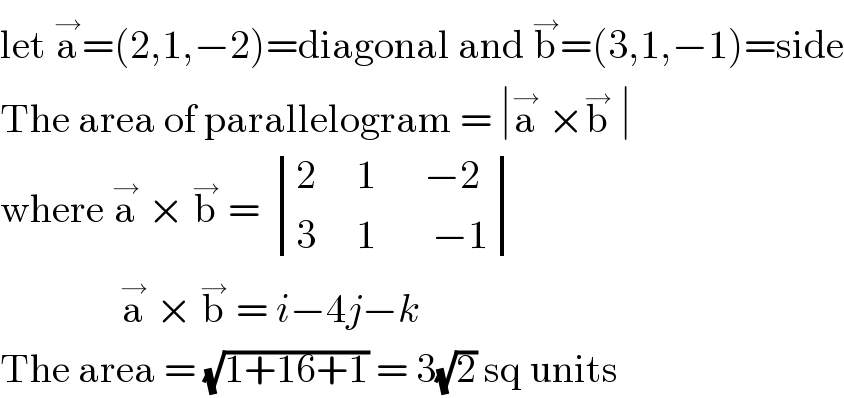
$$\mathrm{let}\:\overset{\rightarrow} {\mathrm{a}}=\left(\mathrm{2},\mathrm{1},−\mathrm{2}\right)=\mathrm{diagonal}\:\mathrm{and}\:\overset{\rightarrow} {\mathrm{b}}=\left(\mathrm{3},\mathrm{1},−\mathrm{1}\right)=\mathrm{side} \\ $$$$\mathrm{The}\:\mathrm{area}\:\mathrm{of}\:\mathrm{parallelogram}\:=\:\mid\overset{\rightarrow} {\mathrm{a}}\:×\overset{\rightarrow} {\mathrm{b}}\:\mid \\ $$$$\mathrm{where}\:\overset{\rightarrow} {\mathrm{a}}\:×\:\overset{\rightarrow} {\mathrm{b}}\:=\:\begin{vmatrix}{\mathrm{2}\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:−\mathrm{2}}\\{\mathrm{3}\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:−\mathrm{1}}\end{vmatrix} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\overset{\rightarrow} {\mathrm{a}}\:×\:\overset{\rightarrow} {\mathrm{b}}\:=\:{i}−\mathrm{4}{j}−{k} \\ $$$$\mathrm{The}\:\mathrm{area}\:=\:\sqrt{\mathrm{1}+\mathrm{16}+\mathrm{1}}\:=\:\mathrm{3}\sqrt{\mathrm{2}}\:\mathrm{sq}\:\mathrm{units} \\ $$
