
Question Number 118002 by mmmmmm1 last updated on 14/Oct/20
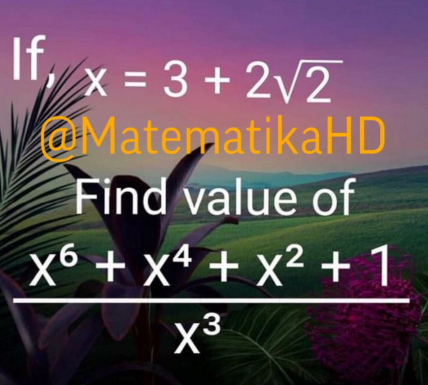
Answered by TANMAY PANACEA last updated on 14/Oct/20
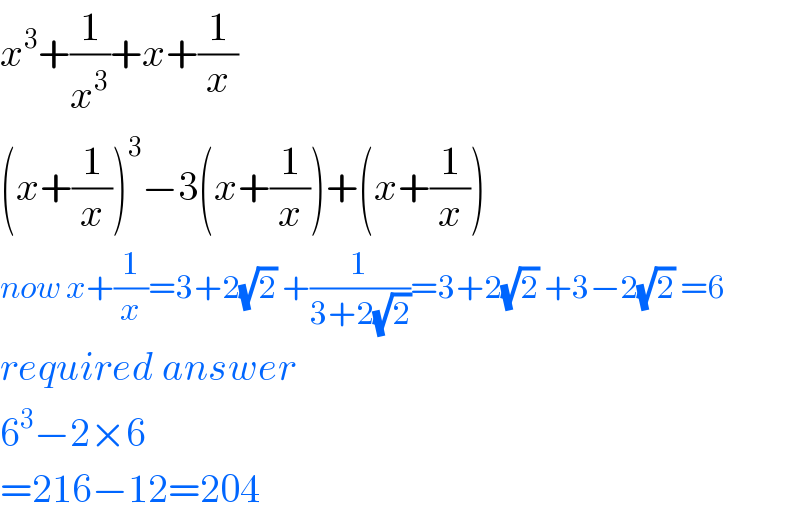
$${x}^{\mathrm{3}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}} }+{x}+\frac{\mathrm{1}}{{x}} \\ $$$$\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{3}} −\mathrm{3}\left({x}+\frac{\mathrm{1}}{{x}}\right)+\left({x}+\frac{\mathrm{1}}{{x}}\right) \\ $$$${now}\:{x}+\frac{\mathrm{1}}{{x}}=\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}}=\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\:+\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}\:=\mathrm{6} \\ $$$${required}\:{answer} \\ $$$$\mathrm{6}^{\mathrm{3}} −\mathrm{2}×\mathrm{6} \\ $$$$=\mathrm{216}−\mathrm{12}=\mathrm{204} \\ $$
