
Question Number 117817 by peter frank last updated on 13/Oct/20
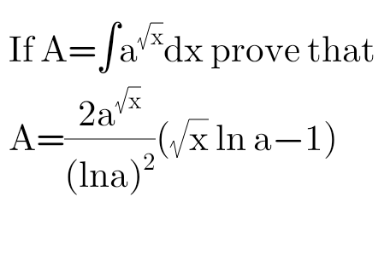
Commented by Lordose last updated on 13/Oct/20
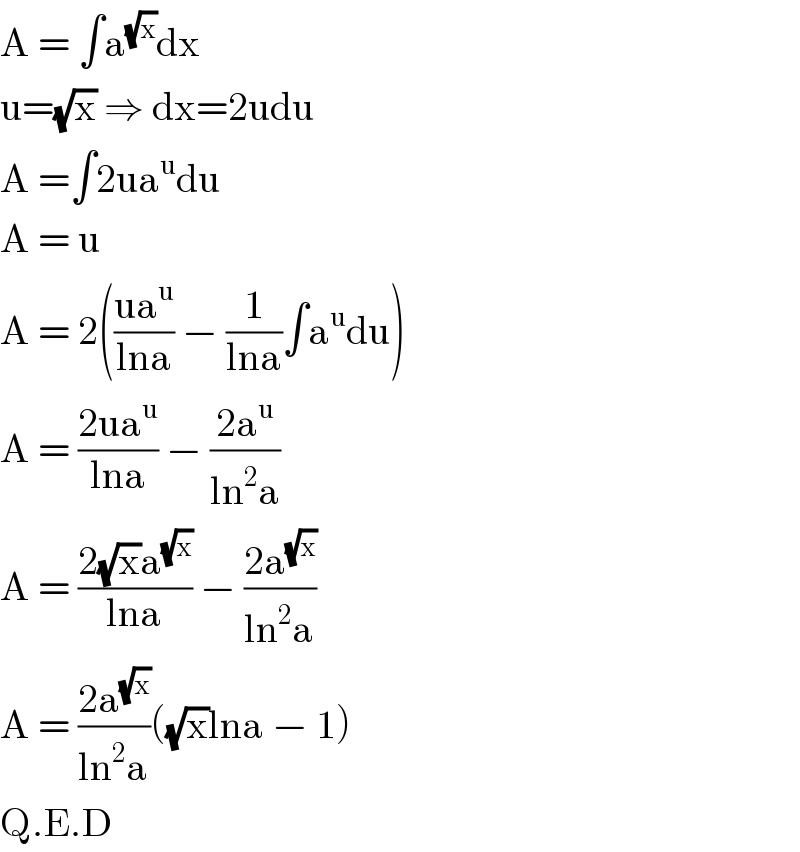
$$\mathrm{A}\:=\:\int\mathrm{a}^{\sqrt{\mathrm{x}}} \mathrm{dx} \\ $$$$\mathrm{u}=\sqrt{\mathrm{x}}\:\Rightarrow\:\mathrm{dx}=\mathrm{2udu} \\ $$$$\mathrm{A}\:=\int\mathrm{2ua}^{\mathrm{u}} \mathrm{du} \\ $$$$\mathrm{A}\:=\:\mathrm{u} \\ $$$$\mathrm{A}\:=\:\mathrm{2}\left(\frac{\mathrm{ua}^{\mathrm{u}} }{\mathrm{lna}}\:−\:\frac{\mathrm{1}}{\mathrm{lna}}\int\mathrm{a}^{\mathrm{u}} \mathrm{du}\right) \\ $$$$\mathrm{A}\:=\:\frac{\mathrm{2ua}^{\mathrm{u}} }{\mathrm{lna}}\:−\:\frac{\mathrm{2a}^{\mathrm{u}} }{\mathrm{ln}^{\mathrm{2}} \mathrm{a}} \\ $$$$\mathrm{A}\:=\:\frac{\mathrm{2}\sqrt{\mathrm{x}}\mathrm{a}^{\sqrt{\mathrm{x}}} }{\mathrm{lna}}\:−\:\frac{\mathrm{2a}^{\sqrt{\mathrm{x}}} }{\mathrm{ln}^{\mathrm{2}} \mathrm{a}} \\ $$$$\mathrm{A}\:=\:\frac{\mathrm{2a}^{\sqrt{\mathrm{x}}} }{\mathrm{ln}^{\mathrm{2}} \mathrm{a}}\left(\sqrt{\mathrm{x}}\mathrm{lna}\:−\:\mathrm{1}\right) \\ $$$$\mathrm{Q}.\mathrm{E}.\mathrm{D} \\ $$
Answered by snipers237 last updated on 13/Oct/20
![A=∫2(√x) a^(√x) (dx/(2(√x))) =∫ 2u e^(ulna) du u=(√x) by parts f′=e^(ulna) f=(a^u /(lna)) g=2u g′=2 A=[((2u)/(lna)) a^u ]−(2/(lna))∫a^u du =[((2u)/(lna))a^u −(2/((lna)^2 ))a^u ]+cte LFYTC](Q117821.png)
$${A}=\int\mathrm{2}\sqrt{{x}}\:\:{a}^{\sqrt{{x}}} \:\frac{{dx}}{\mathrm{2}\sqrt{{x}}}\:\:=\int\:\mathrm{2}{u}\:{e}^{{ulna}} {du}\:\:\:\:\:{u}=\sqrt{{x}}\: \\ $$$${by}\:{parts}\:\:{f}'={e}^{{ulna}} \:\:{f}=\frac{{a}^{{u}} }{{lna}}\:\:\:{g}=\mathrm{2}{u}\:\:\:{g}'=\mathrm{2} \\ $$$${A}=\left[\frac{\mathrm{2}{u}}{{lna}}\:{a}^{{u}} \right]−\frac{\mathrm{2}}{{lna}}\int{a}^{{u}} {du} \\ $$$$\:\:\:=\left[\frac{\mathrm{2}{u}}{{lna}}{a}^{{u}} −\frac{\mathrm{2}}{\left({lna}\right)^{\mathrm{2}} }{a}^{{u}} \right]+{cte} \\ $$$${LFYTC} \\ $$
Answered by mathmax by abdo last updated on 13/Oct/20
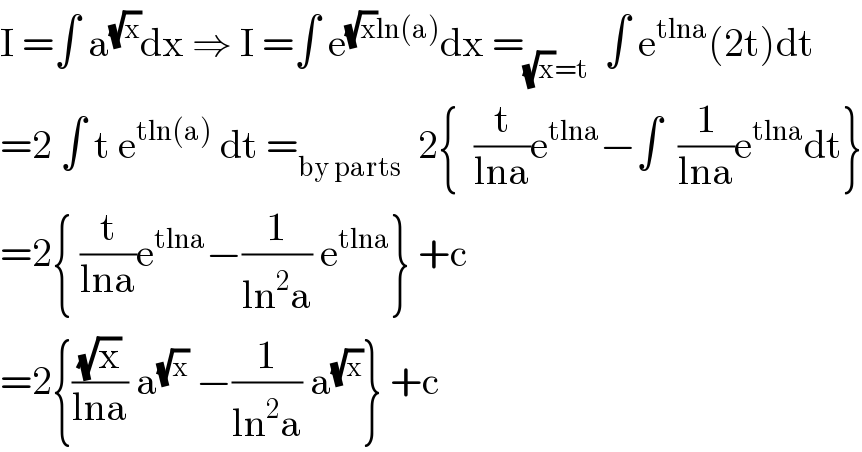
$$\mathrm{I}\:=\int\:\mathrm{a}^{\sqrt{\mathrm{x}}} \mathrm{dx}\:\Rightarrow\:\mathrm{I}\:=\int\:\mathrm{e}^{\sqrt{\mathrm{x}}\mathrm{ln}\left(\mathrm{a}\right)} \mathrm{dx}\:=_{\sqrt{\mathrm{x}}=\mathrm{t}} \:\:\int\:\mathrm{e}^{\mathrm{tlna}} \left(\mathrm{2t}\right)\mathrm{dt} \\ $$$$=\mathrm{2}\:\int\:\mathrm{t}\:\mathrm{e}^{\mathrm{tln}\left(\mathrm{a}\right)} \:\mathrm{dt}\:=_{\mathrm{by}\:\mathrm{parts}} \:\:\mathrm{2}\left\{\:\:\frac{\mathrm{t}}{\mathrm{lna}}\mathrm{e}^{\mathrm{tlna}} −\int\:\:\frac{\mathrm{1}}{\mathrm{lna}}\mathrm{e}^{\mathrm{tlna}} \mathrm{dt}\right\} \\ $$$$=\mathrm{2}\left\{\:\frac{\mathrm{t}}{\mathrm{lna}}\mathrm{e}^{\mathrm{tlna}} −\frac{\mathrm{1}}{\mathrm{ln}^{\mathrm{2}} \mathrm{a}}\:\mathrm{e}^{\mathrm{tlna}} \right\}\:+\mathrm{c} \\ $$$$=\mathrm{2}\left\{\frac{\sqrt{\mathrm{x}}}{\mathrm{lna}}\:\mathrm{a}^{\sqrt{\mathrm{x}}} \:−\frac{\mathrm{1}}{\mathrm{ln}^{\mathrm{2}} \mathrm{a}}\:\mathrm{a}^{\sqrt{\mathrm{x}}} \right\}\:+\mathrm{c} \\ $$
Commented by peter frank last updated on 14/Oct/20
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{both} \\ $$
