
Question Number 117344 by bemath last updated on 11/Oct/20

Commented by bemath last updated on 11/Oct/20
$$\mathrm{yes}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{think}\:\mathrm{this}\:\mathrm{question} \\ $$$$\mathrm{wrong} \\ $$
Commented by bemath last updated on 11/Oct/20

$$\mathrm{anyone}\:\mathrm{can}\:\mathrm{explain}\:\mathrm{me},\:\mathrm{what}\:\mathrm{the} \\ $$$$\mathrm{meaning}\:\mathrm{this}\:\mathrm{question} \\ $$
Commented by bemath last updated on 11/Oct/20

$$\mathrm{Evaluate}\:\mathrm{this}\:\mathrm{limit}\:\mathrm{for}\:\mathrm{the}\:\mathrm{given}\: \\ $$$$\mathrm{value}\:\mathrm{of}\:\mathrm{x}\:\mathrm{and}\:\mathrm{function}\:\mathrm{f}\:. \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{3}^{\sqrt{\mathrm{x}}\:} +\mathrm{5}\:,\:\mathrm{x}=\mathrm{16} \\ $$
Commented by Olaf last updated on 11/Oct/20
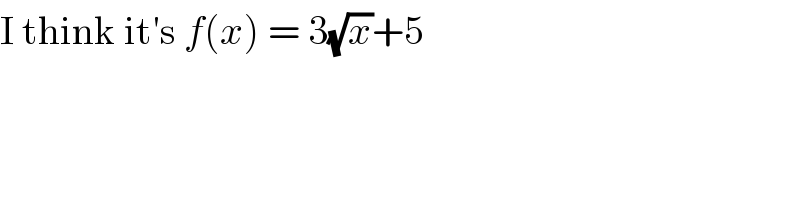
$$\mathrm{I}\:\mathrm{think}\:\mathrm{it}'\mathrm{s}\:{f}\left({x}\right)\:=\:\mathrm{3}\sqrt{{x}}+\mathrm{5} \\ $$
Answered by Olaf last updated on 11/Oct/20

$$ \\ $$$${f}\left(\mathrm{16}+{h}\right)\:=\:\mathrm{3}\sqrt{\mathrm{16}+{h}}+\mathrm{5} \\ $$$${f}\left(\mathrm{16}+{h}\right)\:=\:\mathrm{3}×\mathrm{4}\sqrt{\mathrm{1}+\frac{{h}}{\mathrm{16}}}+\mathrm{5} \\ $$$${f}\left(\mathrm{16}+{h}\right)\:\underset{\mathrm{0}} {\sim}\:\mathrm{12}\left(\mathrm{1}+\frac{{h}}{\mathrm{32}}\right)+\mathrm{5} \\ $$$$\frac{{f}\left(\mathrm{16}+{h}\right)−{f}\left(\mathrm{16}\right)}{{h}}\:\underset{\mathrm{0}} {\sim}\:\frac{\mathrm{12}\left(\mathrm{1}+\frac{{h}}{\mathrm{32}}\right)+\mathrm{5}−\left(\mathrm{12}+\mathrm{5}\right)}{{h}} \\ $$$$\frac{{f}\left(\mathrm{16}+{h}\right)−{f}\left(\mathrm{16}\right)}{{h}}\:\underset{\mathrm{0}} {\sim}\:\frac{\mathrm{12}\frac{{h}}{\mathrm{32}}}{{h}}\:=\:\frac{\mathrm{3}}{\mathrm{8}} \\ $$$$\left(\mathrm{we}\:\mathrm{verify}\:\mathrm{the}\:\mathrm{result}\:\mathrm{with}\:{f}'\left(\mathrm{16}\right)\:=\:\frac{\mathrm{3}}{\mathrm{2}\sqrt{\mathrm{16}}}\:=\:\frac{\mathrm{3}}{\mathrm{8}}\right) \\ $$
