
Question Number 117143 by aurpeyz last updated on 09/Oct/20
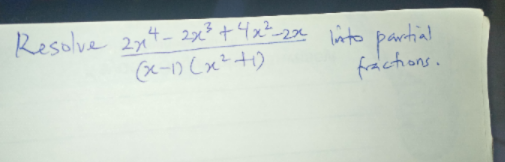
Answered by prakash jain last updated on 13/Oct/20
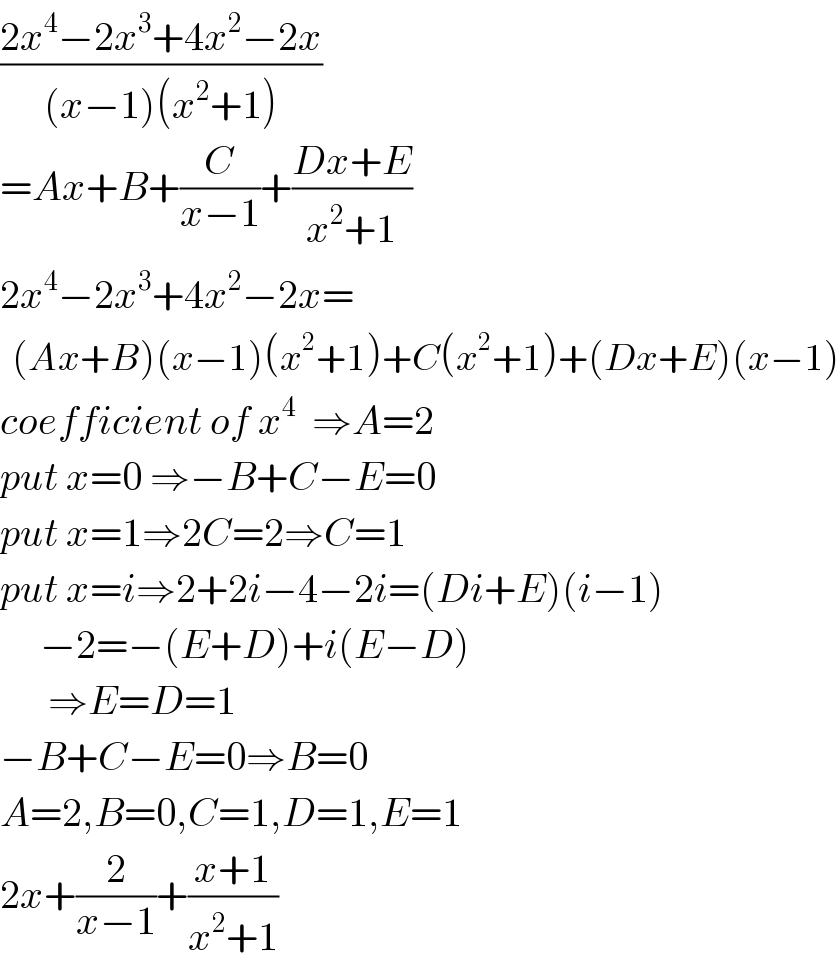
$$\frac{\mathrm{2}{x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{3}} +\mathrm{4}{x}^{\mathrm{2}} −\mathrm{2}{x}}{\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$={Ax}+{B}+\frac{{C}}{{x}−\mathrm{1}}+\frac{{Dx}+{E}}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\mathrm{2}{x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{3}} +\mathrm{4}{x}^{\mathrm{2}} −\mathrm{2}{x}= \\ $$$$\:\:\left({Ax}+{B}\right)\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)+{C}\left({x}^{\mathrm{2}} +\mathrm{1}\right)+\left({Dx}+{E}\right)\left({x}−\mathrm{1}\right) \\ $$$${coefficient}\:{of}\:{x}^{\mathrm{4}} \:\:\Rightarrow{A}=\mathrm{2} \\ $$$${put}\:{x}=\mathrm{0}\:\Rightarrow−{B}+{C}−{E}=\mathrm{0}\:\:\: \\ $$$${put}\:{x}=\mathrm{1}\Rightarrow\mathrm{2}{C}=\mathrm{2}\Rightarrow{C}=\mathrm{1} \\ $$$${put}\:{x}={i}\Rightarrow\mathrm{2}+\mathrm{2}{i}−\mathrm{4}−\mathrm{2}{i}=\left({Di}+{E}\right)\left({i}−\mathrm{1}\right) \\ $$$$\:\:\:\:\:−\mathrm{2}=−\left({E}+{D}\right)+{i}\left({E}−{D}\right) \\ $$$$\:\:\:\:\:\:\Rightarrow{E}={D}=\mathrm{1} \\ $$$$−{B}+{C}−{E}=\mathrm{0}\Rightarrow{B}=\mathrm{0} \\ $$$${A}=\mathrm{2},{B}=\mathrm{0},{C}=\mathrm{1},{D}=\mathrm{1},{E}=\mathrm{1} \\ $$$$\mathrm{2}{x}+\frac{\mathrm{2}}{{x}−\mathrm{1}}+\frac{{x}+\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$
