
Question Number 116997 by mathdave last updated on 08/Oct/20
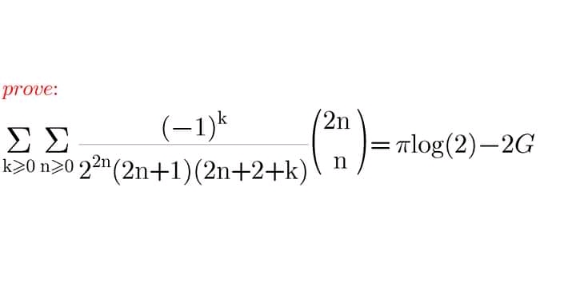
Answered by Olaf last updated on 09/Oct/20
![(1/((2n+1)(2n+2+k))) = (1/(k+1))[(1/(2n+1))−(1/(2n+2+k))] S = Σ_(k=0) ^∞ (((−1)^k )/(k+1))Σ_(n=0) ^∞ [(C_(2n) ^n /(2^(2n) (2n+1)))−(C_(2n) ^n /(2^(2n) (2n+2+k)))] S = Σ_(n=0) ^∞ [(C_(2n) ^n /(2^(2n) (2n+1)))Σ_(k=0) ^∞ (((−1)^k )/(k+1))−(C_(2n) ^n /2^(2n) )Σ_(k=0) ^∞ (((−1)^k )/(2n+2+k))] S = Σ_(n=0) ^∞ [−(C_(2n) ^n /(2^(2n) (2n+1)))Σ_(k=0) ^∞ (((−1)^(k+1) )/(k+1))−(C_(2n) ^n /2^(2n) )Σ_(k=0) ^∞ (((−1)^(2n+2+k) )/(2n+2+k))] S = Σ_(n=0) ^∞ [−(C_(2n) ^n /(2^(2n) (2n+1)))Σ_(k=1) ^∞ (((−1)^k )/k)−(C_(2n) ^n /2^(2n) )Σ_(k=2n+2) ^∞ (((−1)^k )/k)] Σ_(k=0) ^∞ (((−1)^k )/k) = −ln2 S = Σ_(n=0) ^∞ [ln2(C_(2n) ^n /(2^(2n) (2n+1)))−(C_(2n) ^n /2^(2n) )(−ln2−Σ_(k=1) ^(k=2n+1) (((−1)^k )/k))] S = ln2Σ_(n=0) ^∞ (C_(2n) ^n /2^(2n) )((1/(2n+1))+1)+Σ_(n=0) ^∞ (C_(2n) ^n /2^(2n) )Σ_(k=1) ^(k=2n+1) (((−1)^k )/k) S = ln2Σ_(n=0) ^∞ (C_(2n) ^n /2^(2n) ).((2n+2)/(2n+1))+Σ_(n=0) ^∞ (C_(2n) ^n /2^(2n) )Σ_(k=1) ^(k=2n+1) (((−1)^k )/k) work in progress...](Q117062.png)
$$\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{2}+{k}\right)}\:=\:\frac{\mathrm{1}}{{k}+\mathrm{1}}\left[\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{2}+{k}}\right] \\ $$$$\mathrm{S}\:=\:\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}+\mathrm{1}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left[\frac{\mathrm{C}_{\mathrm{2}{n}} ^{{n}} }{\mathrm{2}^{\mathrm{2}{n}} \left(\mathrm{2}{n}+\mathrm{1}\right)}−\frac{\mathrm{C}_{\mathrm{2}{n}} ^{{n}} }{\mathrm{2}^{\mathrm{2}{n}} \left(\mathrm{2}{n}+\mathrm{2}+{k}\right)}\right] \\ $$$$\mathrm{S}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left[\frac{\mathrm{C}_{\mathrm{2}{n}} ^{{n}} }{\mathrm{2}^{\mathrm{2}{n}} \left(\mathrm{2}{n}+\mathrm{1}\right)}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}+\mathrm{1}}−\frac{\mathrm{C}_{\mathrm{2}{n}} ^{{n}} }{\mathrm{2}^{\mathrm{2}{n}} }\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}{n}+\mathrm{2}+{k}}\right] \\ $$$$\mathrm{S}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left[−\frac{\mathrm{C}_{\mathrm{2}{n}} ^{{n}} }{\mathrm{2}^{\mathrm{2}{n}} \left(\mathrm{2}{n}+\mathrm{1}\right)}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} }{{k}+\mathrm{1}}−\frac{\mathrm{C}_{\mathrm{2}{n}} ^{{n}} }{\mathrm{2}^{\mathrm{2}{n}} }\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{2}{n}+\mathrm{2}+{k}} }{\mathrm{2}{n}+\mathrm{2}+{k}}\right] \\ $$$$\mathrm{S}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left[−\frac{\mathrm{C}_{\mathrm{2}{n}} ^{{n}} }{\mathrm{2}^{\mathrm{2}{n}} \left(\mathrm{2}{n}+\mathrm{1}\right)}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}}−\frac{\mathrm{C}_{\mathrm{2}{n}} ^{{n}} }{\mathrm{2}^{\mathrm{2}{n}} }\underset{{k}=\mathrm{2}{n}+\mathrm{2}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}}\right] \\ $$$$\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}}\:=\:−\mathrm{ln2} \\ $$$$\mathrm{S}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left[\mathrm{ln2}\frac{\mathrm{C}_{\mathrm{2}{n}} ^{{n}} }{\mathrm{2}^{\mathrm{2}{n}} \left(\mathrm{2}{n}+\mathrm{1}\right)}−\frac{\mathrm{C}_{\mathrm{2}{n}} ^{{n}} }{\mathrm{2}^{\mathrm{2}{n}} }\left(−\mathrm{ln2}−\underset{{k}=\mathrm{1}} {\overset{{k}=\mathrm{2}{n}+\mathrm{1}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}}\right)\right] \\ $$$$\mathrm{S}\:=\:\mathrm{ln2}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{C}_{\mathrm{2}{n}} ^{{n}} }{\mathrm{2}^{\mathrm{2}{n}} }\left(\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}+\mathrm{1}\right)+\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{C}_{\mathrm{2}{n}} ^{{n}} }{\mathrm{2}^{\mathrm{2}{n}} }\underset{{k}=\mathrm{1}} {\overset{{k}=\mathrm{2}{n}+\mathrm{1}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}} \\ $$$$\mathrm{S}\:=\:\mathrm{ln2}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{C}_{\mathrm{2}{n}} ^{{n}} }{\mathrm{2}^{\mathrm{2}{n}} }.\frac{\mathrm{2}{n}+\mathrm{2}}{\mathrm{2}{n}+\mathrm{1}}+\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{C}_{\mathrm{2}{n}} ^{{n}} }{\mathrm{2}^{\mathrm{2}{n}} }\underset{{k}=\mathrm{1}} {\overset{{k}=\mathrm{2}{n}+\mathrm{1}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}} \\ $$$${work}\:{in}\:{progress}... \\ $$
