
Question Number 116633 by zakirullah last updated on 05/Oct/20
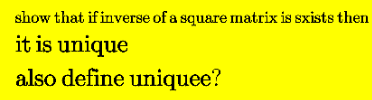
Answered by Olaf last updated on 05/Oct/20
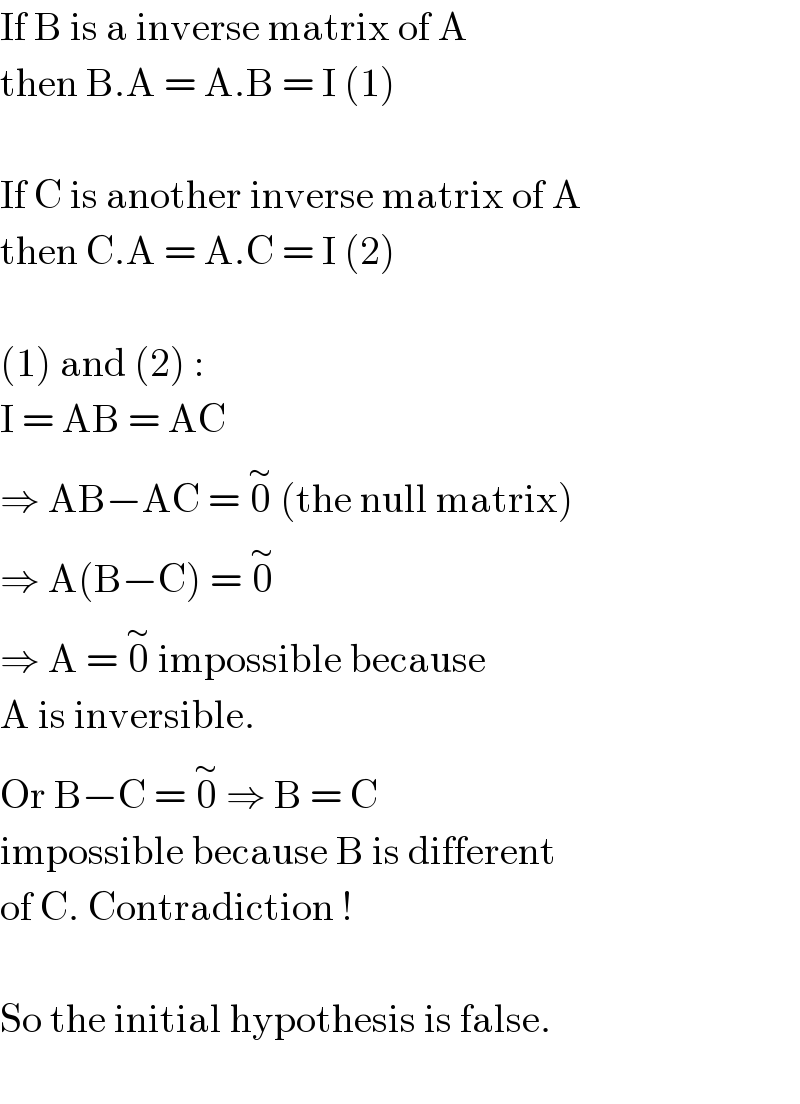
$$\mathrm{If}\:\mathrm{B}\:\mathrm{is}\:\mathrm{a}\:\mathrm{inverse}\:\mathrm{matrix}\:\mathrm{of}\:\mathrm{A} \\ $$$$\mathrm{then}\:\mathrm{B}.\mathrm{A}\:=\:\mathrm{A}.\mathrm{B}\:=\:\mathrm{I}\:\left(\mathrm{1}\right) \\ $$$$ \\ $$$$\mathrm{If}\:\mathrm{C}\:\mathrm{is}\:\mathrm{another}\:\mathrm{inverse}\:\mathrm{matrix}\:\mathrm{of}\:\mathrm{A} \\ $$$$\mathrm{then}\:\mathrm{C}.\mathrm{A}\:=\:\mathrm{A}.\mathrm{C}\:=\:\mathrm{I}\:\left(\mathrm{2}\right) \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\:\mathrm{and}\:\left(\mathrm{2}\right)\:: \\ $$$$\mathrm{I}\:=\:\mathrm{AB}\:=\:\mathrm{AC} \\ $$$$\Rightarrow\:\mathrm{AB}−\mathrm{AC}\:=\:\overset{\sim} {\mathrm{0}}\:\left(\mathrm{the}\:\mathrm{null}\:\mathrm{matrix}\right) \\ $$$$\Rightarrow\:\mathrm{A}\left(\mathrm{B}−\mathrm{C}\right)\:=\:\overset{\sim} {\mathrm{0}} \\ $$$$\Rightarrow\:\mathrm{A}\:=\:\overset{\sim} {\mathrm{0}}\:\mathrm{impossible}\:\mathrm{because} \\ $$$$\mathrm{A}\:\mathrm{is}\:\mathrm{inversible}. \\ $$$$\mathrm{Or}\:\mathrm{B}−\mathrm{C}\:=\:\overset{\sim} {\mathrm{0}}\:\Rightarrow\:\mathrm{B}\:=\:\mathrm{C} \\ $$$$\mathrm{impossible}\:\mathrm{because}\:\mathrm{B}\:\mathrm{is}\:\mathrm{different} \\ $$$$\mathrm{of}\:\mathrm{C}.\:\mathrm{Contradiction}\:! \\ $$$$ \\ $$$$\mathrm{So}\:\mathrm{the}\:\mathrm{initial}\:\mathrm{hypothesis}\:\mathrm{is}\:\mathrm{false}. \\ $$$$ \\ $$
