
Question Number 116290 by ravisoni last updated on 02/Oct/20

Commented by Dwaipayan Shikari last updated on 03/Oct/20
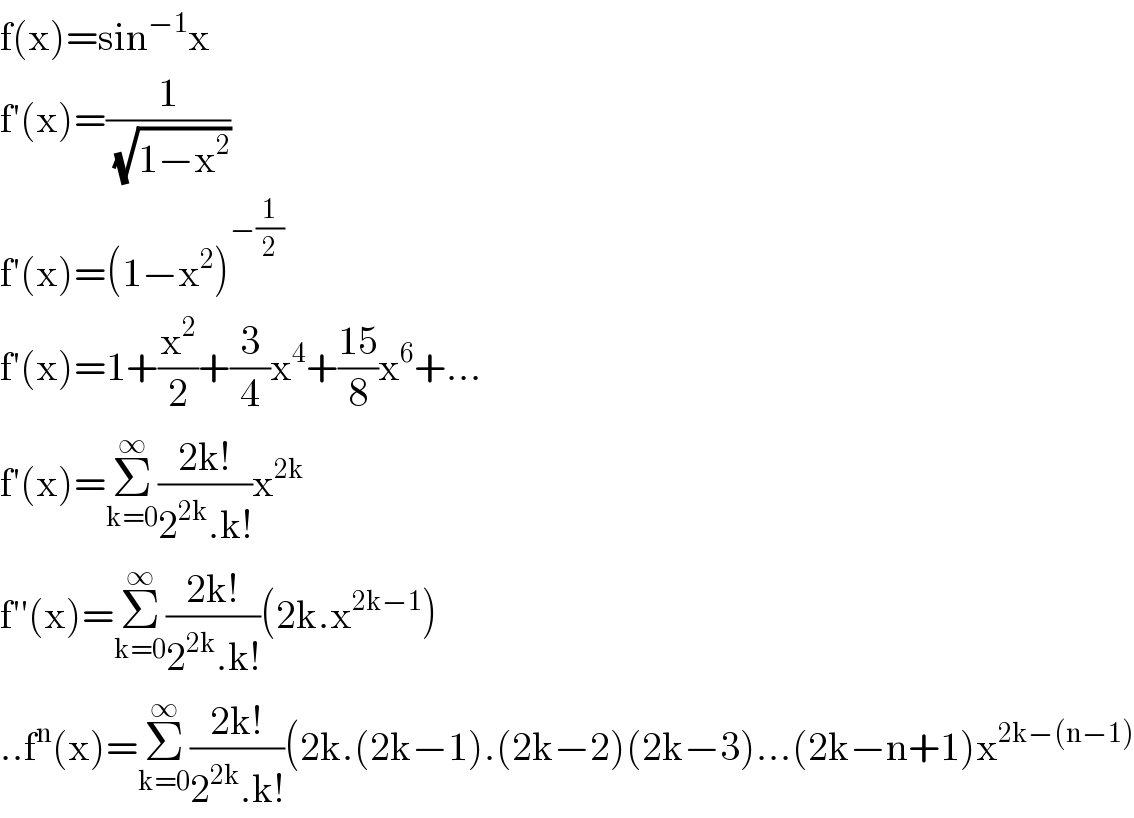
$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{sin}^{−\mathrm{1}} \mathrm{x} \\ $$$$\mathrm{f}'\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }} \\ $$$$\mathrm{f}'\left(\mathrm{x}\right)=\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\mathrm{f}'\left(\mathrm{x}\right)=\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{4}}\mathrm{x}^{\mathrm{4}} +\frac{\mathrm{15}}{\mathrm{8}}\mathrm{x}^{\mathrm{6}} +... \\ $$$$\mathrm{f}'\left(\mathrm{x}\right)=\underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{2k}!}{\mathrm{2}^{\mathrm{2k}} .\mathrm{k}!}\mathrm{x}^{\mathrm{2k}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\mathrm{f}''\left(\mathrm{x}\right)=\underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{2k}!}{\mathrm{2}^{\mathrm{2k}} .\mathrm{k}!}\left(\mathrm{2k}.\mathrm{x}^{\mathrm{2k}−\mathrm{1}} \right) \\ $$$$..\mathrm{f}^{\mathrm{n}} \left(\mathrm{x}\right)=\underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{2k}!}{\mathrm{2}^{\mathrm{2k}} .\mathrm{k}!}\left(\mathrm{2k}.\left(\mathrm{2k}−\mathrm{1}\right).\left(\mathrm{2k}−\mathrm{2}\right)\left(\mathrm{2k}−\mathrm{3}\right)...\left(\mathrm{2k}−\mathrm{n}+\mathrm{1}\right)\mathrm{x}^{\mathrm{2k}−\left(\mathrm{n}−\mathrm{1}\right)} \right. \\ $$
