Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 115997 by bemath last updated on 30/Sep/20

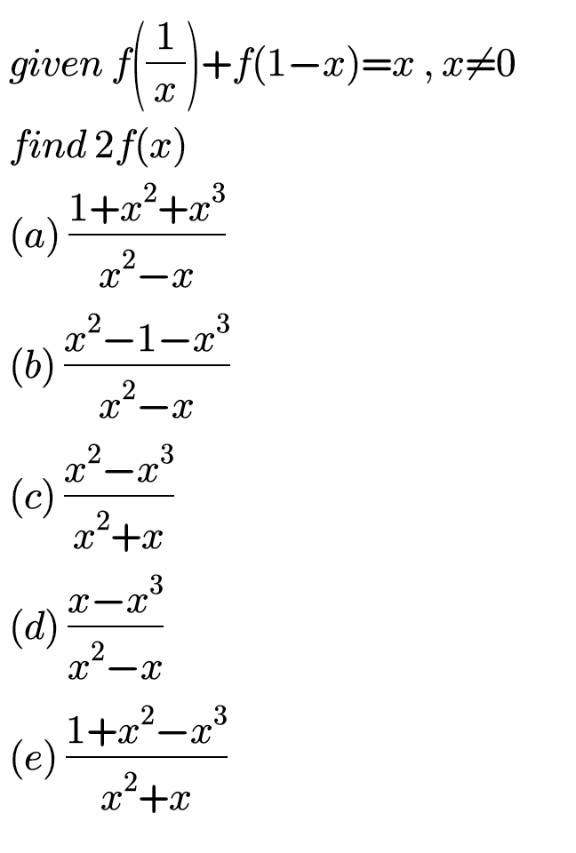
Answered by bobhans last updated on 30/Sep/20

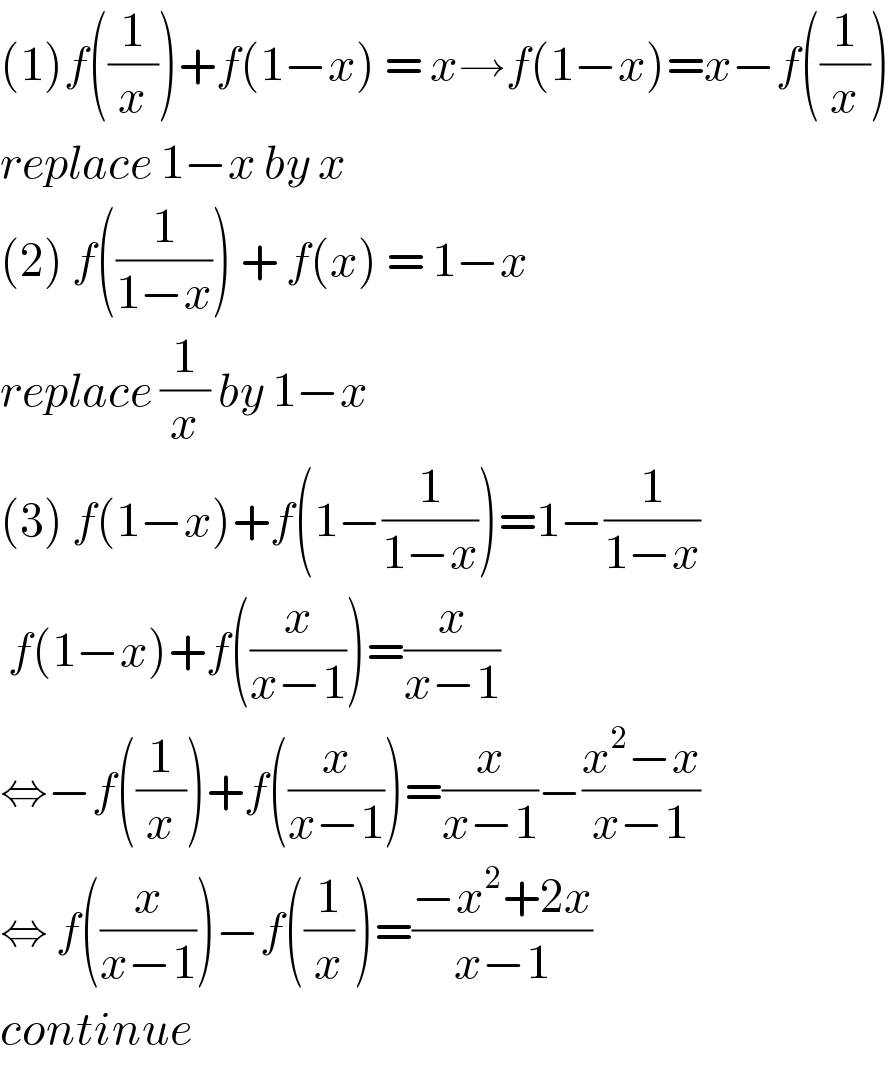
(1)f((1/x))+f(1−x) = x→f(1−x)=x−f((1/x)) replace 1−x by x (2) f((1/(1−x))) + f(x) = 1−x replace (1/x) by 1−x (3) f(1−x)+f(1−(1/(1−x)))=1−(1/(1−x)) f(1−x)+f((x/(x−1)))=(x/(x−1)) ⇔−f((1/x))+f((x/(x−1)))=(x/(x−1))−((x^2 −x)/(x−1)) ⇔ f((x/(x−1)))−f((1/x))=((−x^2 +2x)/(x−1)) continue

$$\left(\mathrm{1}\right){f}\left(\frac{\mathrm{1}}{{x}}\right)+{f}\left(\mathrm{1}−{x}\right)\:=\:{x}\rightarrow{f}\left(\mathrm{1}−{x}\right)={x}−{f}\left(\frac{\mathrm{1}}{{x}}\right) \\ $$$${replace}\:\mathrm{1}−{x}\:{by}\:{x} \\ $$$$\left(\mathrm{2}\right)\:{f}\left(\frac{\mathrm{1}}{\mathrm{1}−{x}}\right)\:+\:{f}\left({x}\right)\:=\:\mathrm{1}−{x} \\ $$$${replace}\:\frac{\mathrm{1}}{{x}}\:{by}\:\mathrm{1}−{x}\: \\ $$$$\left(\mathrm{3}\right)\:{f}\left(\mathrm{1}−{x}\right)+{f}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}−{x}}\right)=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}−{x}} \\ $$$$\:{f}\left(\mathrm{1}−{x}\right)+{f}\left(\frac{{x}}{{x}−\mathrm{1}}\right)=\frac{{x}}{{x}−\mathrm{1}} \\ $$$$\Leftrightarrow−{f}\left(\frac{\mathrm{1}}{{x}}\right)+{f}\left(\frac{{x}}{{x}−\mathrm{1}}\right)=\frac{{x}}{{x}−\mathrm{1}}−\frac{{x}^{\mathrm{2}} −{x}}{{x}−\mathrm{1}} \\ $$$$\Leftrightarrow\:{f}\left(\frac{{x}}{{x}−\mathrm{1}}\right)−{f}\left(\frac{\mathrm{1}}{{x}}\right)=\frac{−{x}^{\mathrm{2}} +\mathrm{2}{x}}{{x}−\mathrm{1}} \\ $$$${continue} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com