
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 115988 by bemath last updated on 30/Sep/20

Commented by mr W last updated on 01/Oct/20
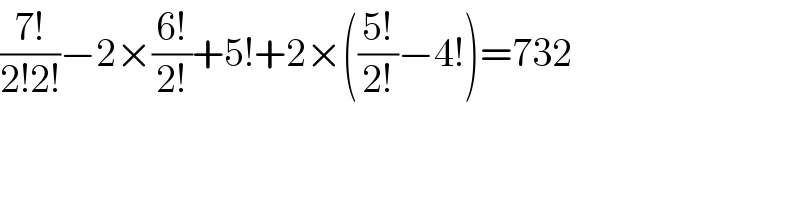
$$\frac{\mathrm{7}!}{\mathrm{2}!\mathrm{2}!}−\mathrm{2}×\frac{\mathrm{6}!}{\mathrm{2}!}+\mathrm{5}!+\mathrm{2}×\left(\frac{\mathrm{5}!}{\mathrm{2}!}−\mathrm{4}!\right)=\mathrm{732} \\ $$
Commented by bemath last updated on 01/Oct/20
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{no}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{correct}\:\mathrm{sir} \\ $$
Answered by mr W last updated on 01/Oct/20
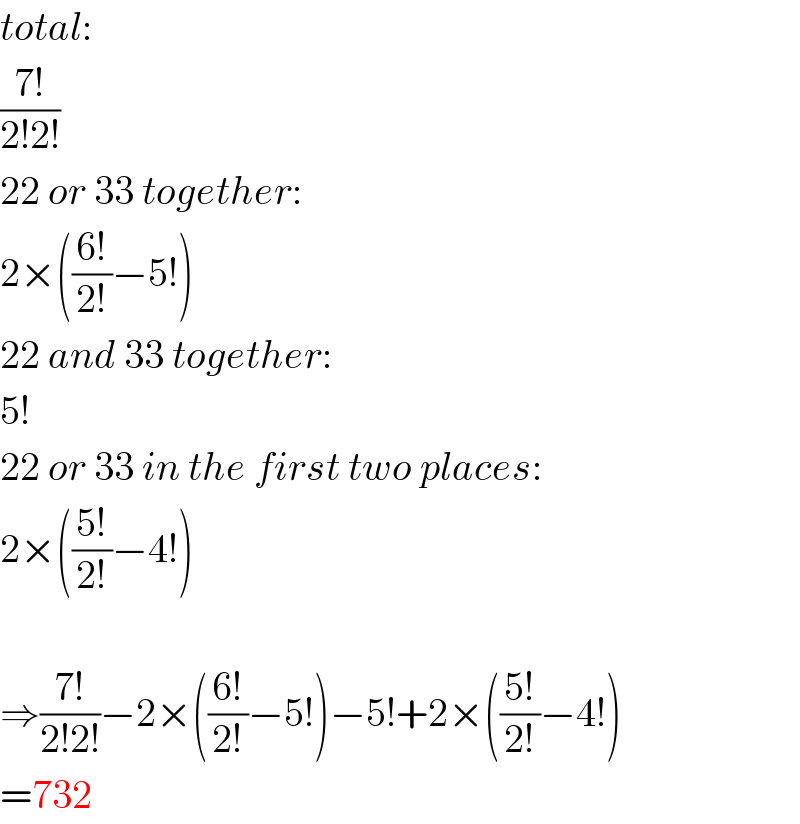
$${total}: \\ $$$$\frac{\mathrm{7}!}{\mathrm{2}!\mathrm{2}!} \\ $$$$\mathrm{22}\:{or}\:\mathrm{33}\:{together}: \\ $$$$\mathrm{2}×\left(\frac{\mathrm{6}!}{\mathrm{2}!}−\mathrm{5}!\right) \\ $$$$\mathrm{22}\:{and}\:\mathrm{33}\:{together}: \\ $$$$\mathrm{5}! \\ $$$$\mathrm{22}\:{or}\:\mathrm{33}\:{in}\:{the}\:{first}\:{two}\:{places}: \\ $$$$\mathrm{2}×\left(\frac{\mathrm{5}!}{\mathrm{2}!}−\mathrm{4}!\right) \\ $$$$ \\ $$$$\Rightarrow\frac{\mathrm{7}!}{\mathrm{2}!\mathrm{2}!}−\mathrm{2}×\left(\frac{\mathrm{6}!}{\mathrm{2}!}−\mathrm{5}!\right)−\mathrm{5}!+\mathrm{2}×\left(\frac{\mathrm{5}!}{\mathrm{2}!}−\mathrm{4}!\right) \\ $$$$=\mathrm{732} \\ $$
Commented by bemath last updated on 02/Oct/20
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{prof}\:\mathrm{mr}\:\mathrm{W} \\ $$
