Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 115798 by aye48 last updated on 28/Sep/20

Commented by bemath last updated on 29/Sep/20

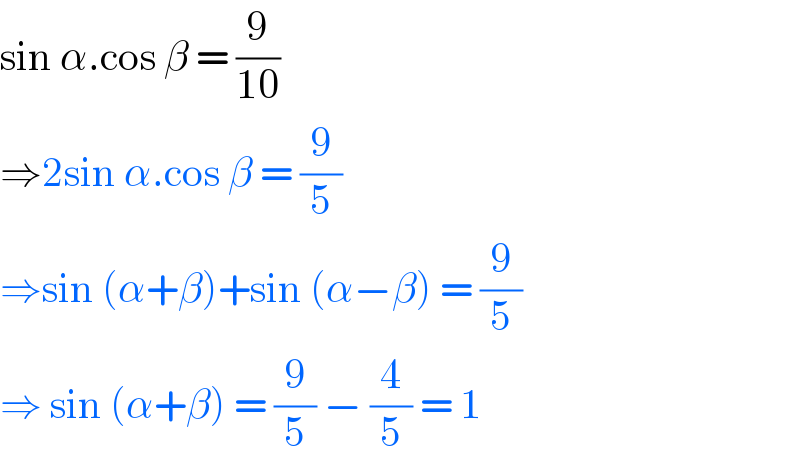
sin α.cos β = (9/(10)) ⇒2sin α.cos β = (9/5) ⇒sin (α+β)+sin (α−β) = (9/5) ⇒ sin (α+β) = (9/5) − (4/5) = 1

$$\mathrm{sin}\:\alpha.\mathrm{cos}\:\beta\:=\:\frac{\mathrm{9}}{\mathrm{10}} \\ $$$$\Rightarrow\mathrm{2sin}\:\alpha.\mathrm{cos}\:\beta\:=\:\frac{\mathrm{9}}{\mathrm{5}} \\ $$$$\Rightarrow\mathrm{sin}\:\left(\alpha+\beta\right)+\mathrm{sin}\:\left(\alpha−\beta\right)\:=\:\frac{\mathrm{9}}{\mathrm{5}} \\ $$$$\Rightarrow\:\mathrm{sin}\:\left(\alpha+\beta\right)\:=\:\frac{\mathrm{9}}{\mathrm{5}}\:−\:\frac{\mathrm{4}}{\mathrm{5}}\:=\:\mathrm{1} \\ $$

Answered by TANMAY PANACEA last updated on 29/Sep/20

sinαcosβ−cosαsinβ=(4/5) cosαsinβ=(9/(10))−(4/5)=(1/(10)) sin(α−β)=(4/5)=sin53^o sin(α+β)=sinαcosβ+cosαsinβ=(9/(10))+(1/(10))=sin90^o =1 α+β=90 α−β=53 α=((90+53)/2)=((143)/2) β=((90−53)/2)=((37)/2) ((tanα)/(tanβ))=((sinαcosβ)/(sinβcosα))=(9/(10))×((10)/1)=9

$${sin}\alpha{cos}\beta−{cos}\alpha{sin}\beta=\frac{\mathrm{4}}{\mathrm{5}} \\ $$$${cos}\alpha{sin}\beta=\frac{\mathrm{9}}{\mathrm{10}}−\frac{\mathrm{4}}{\mathrm{5}}=\frac{\mathrm{1}}{\mathrm{10}} \\ $$$${sin}\left(\alpha−\beta\right)=\frac{\mathrm{4}}{\mathrm{5}}={sin}\mathrm{53}^{{o}} \\ $$$${sin}\left(\alpha+\beta\right)={sin}\alpha{cos}\beta+{cos}\alpha{sin}\beta=\frac{\mathrm{9}}{\mathrm{10}}+\frac{\mathrm{1}}{\mathrm{10}}={sin}\mathrm{90}^{{o}} =\mathrm{1} \\ $$$$\alpha+\beta=\mathrm{90} \\ $$$$\alpha−\beta=\mathrm{53} \\ $$$$\alpha=\frac{\mathrm{90}+\mathrm{53}}{\mathrm{2}}=\frac{\mathrm{143}}{\mathrm{2}} \\ $$$$\beta=\frac{\mathrm{90}−\mathrm{53}}{\mathrm{2}}=\frac{\mathrm{37}}{\mathrm{2}} \\ $$$$\frac{{tan}\alpha}{{tan}\beta}=\frac{{sin}\alpha{cos}\beta}{{sin}\beta{cos}\alpha}=\frac{\mathrm{9}}{\mathrm{10}}×\frac{\mathrm{10}}{\mathrm{1}}=\mathrm{9} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com