Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 115750 by shahria14 last updated on 28/Sep/20

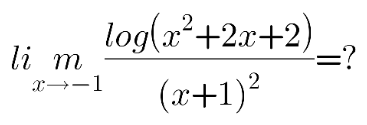
Answered by Dwaipayan Shikari last updated on 28/Sep/20

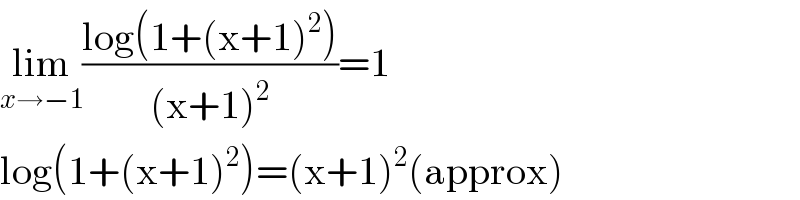
lim_(x→−1) ((log(1+(x+1)^2 ))/((x+1)^2 ))=1 log(1+(x+1)^2 )=(x+1)^2 (approx)

$$\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{log}\left(\mathrm{1}+\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \right)}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }=\mathrm{1} \\ $$$$\mathrm{log}\left(\mathrm{1}+\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \right)=\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{approx}\right) \\ $$

Answered by Ar Brandon last updated on 28/Sep/20

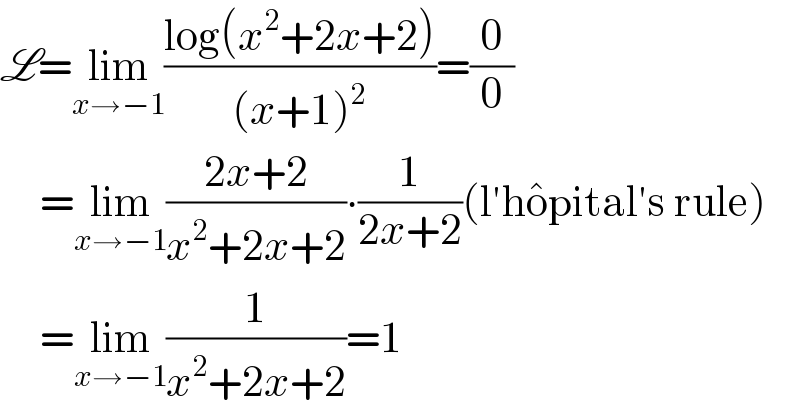
L=lim_(x→−1) ((log(x^2 +2x+2))/((x+1)^2 ))=(0/0) =lim_(x→−1) ((2x+2)/(x^2 +2x+2))∙(1/(2x+2))(l′ho^� pital′s rule) =lim_(x→−1) (1/(x^2 +2x+2))=1

$$\mathscr{L}=\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{log}\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}\right)}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }=\frac{\mathrm{0}}{\mathrm{0}} \\ $$$$\:\:\:\:\:=\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{2}{x}+\mathrm{2}}{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}}\centerdot\frac{\mathrm{1}}{\mathrm{2}{x}+\mathrm{2}}\left(\mathrm{l}'\mathrm{h}\hat {\mathrm{o}pital}'\mathrm{s}\:\mathrm{rule}\right) \\ $$$$\:\:\:\:\:=\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}}=\mathrm{1} \\ $$

Answered by mathmax by abdo last updated on 28/Sep/20

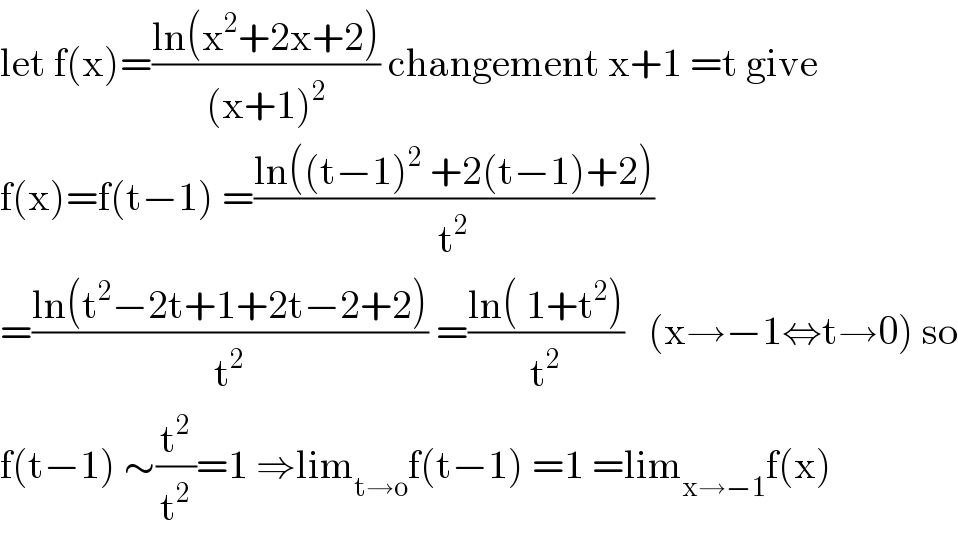
let f(x)=((ln(x^2 +2x+2))/((x+1)^2 )) changement x+1 =t give f(x)=f(t−1) =((ln((t−1)^2 +2(t−1)+2))/t^2 ) =((ln(t^2 −2t+1+2t−2+2))/t^2 ) =((ln( 1+t^2 ))/t^2 ) (x→−1⇔t→0) so f(t−1) ∼(t^2 /t^2 )=1 ⇒lim_(t→o) f(t−1) =1 =lim_(x→−1) f(x)

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{2}\right)}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\:\mathrm{changement}\:\mathrm{x}+\mathrm{1}\:=\mathrm{t}\:\mathrm{give} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{f}\left(\mathrm{t}−\mathrm{1}\right)\:=\frac{\mathrm{ln}\left(\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{2}\left(\mathrm{t}−\mathrm{1}\right)+\mathrm{2}\right)}{\mathrm{t}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{ln}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{2t}+\mathrm{1}+\mathrm{2t}−\mathrm{2}+\mathrm{2}\right)}{\mathrm{t}^{\mathrm{2}} }\:=\frac{\mathrm{ln}\left(\:\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}{\mathrm{t}^{\mathrm{2}} }\:\:\:\left(\mathrm{x}\rightarrow−\mathrm{1}\Leftrightarrow\mathrm{t}\rightarrow\mathrm{0}\right)\:\mathrm{so} \\ $$$$\mathrm{f}\left(\mathrm{t}−\mathrm{1}\right)\:\sim\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{t}^{\mathrm{2}} }=\mathrm{1}\:\Rightarrow\mathrm{lim}_{\mathrm{t}\rightarrow\mathrm{o}} \mathrm{f}\left(\mathrm{t}−\mathrm{1}\right)\:=\mathrm{1}\:=\mathrm{lim}_{\mathrm{x}\rightarrow−\mathrm{1}} \mathrm{f}\left(\mathrm{x}\right) \\ $$

Answered by TANMAY PANACEA last updated on 28/Sep/20

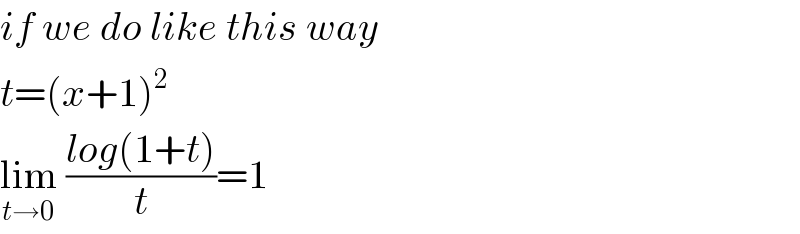
if we do like this way t=(x+1)^2 lim_(t→0) ((log(1+t))/t)=1

$${if}\:{we}\:{do}\:{like}\:{this}\:{way} \\ $$$${t}=\left({x}+\mathrm{1}\right)^{\mathrm{2}} \:\:\:\:\: \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{log}\left(\mathrm{1}+{t}\right)}{{t}}=\mathrm{1} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com