
Question Number 115136 by Algoritm last updated on 23/Sep/20
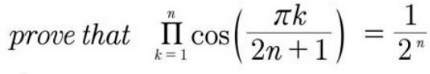
Answered by Olaf last updated on 23/Sep/20

$$\mathrm{sin2}\theta\:=\:\mathrm{2sin}\theta\mathrm{cos}\theta \\ $$$$\mathrm{cos}\theta\:=\:\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{sin2}\theta}{\mathrm{sin}\theta} \\ $$$$\theta\:=\:\frac{{k}\pi}{\mathrm{2}{n}+\mathrm{1}},\:\mathrm{cos}\left(\frac{{k}\pi}{\mathrm{2}{n}+\mathrm{1}}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{sin}\left(\frac{\mathrm{2}{k}\pi}{\mathrm{2}{n}+\mathrm{1}}\right)}{\mathrm{sin}\left(\frac{{k}\pi}{\mathrm{2}{n}+\mathrm{1}}\right)} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}\mathrm{cos}\left(\frac{{k}\pi}{\mathrm{2}{n}+\mathrm{1}}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}\frac{\mathrm{sin}\left(\frac{\mathrm{2}{k}\pi}{\mathrm{2}{n}+\mathrm{1}}\right)}{\mathrm{sin}\left(\frac{{k}\pi}{\mathrm{2}{n}+\mathrm{1}}\right)} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}\mathrm{cos}\left(\frac{{k}\pi}{\mathrm{2}{n}+\mathrm{1}}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}^{{n}} }.\frac{\mathrm{sin}\left(\frac{\mathrm{2}\pi}{\mathrm{2}{n}+\mathrm{1}}\right)}{\mathrm{sin}\left(\frac{\pi}{\mathrm{2}{n}+\mathrm{1}}\right)}×\frac{\mathrm{sin}\left(\frac{\mathrm{4}\pi}{\mathrm{2}{n}+\mathrm{1}}\right)}{\mathrm{sin}\left(\frac{\mathrm{2}\pi}{\mathrm{2}{n}+\mathrm{1}}\right)}...×\frac{\mathrm{sin}\left(\frac{\mathrm{2}\pi{n}}{\mathrm{2}{n}+\mathrm{1}}\right)}{\mathrm{sin}\left(\frac{\pi{n}}{\mathrm{2}{n}+\mathrm{1}}\right)} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}\mathrm{cos}\left(\frac{{k}\pi}{\mathrm{2}{n}+\mathrm{1}}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}^{{n}} }.\frac{\mathrm{sin}\left(\frac{\mathrm{2}\pi{n}}{\mathrm{2}{n}+\mathrm{1}}\right)}{\mathrm{sin}\left(\frac{\pi}{\mathrm{2}{n}+\mathrm{1}}\right)} \\ $$$$\mathrm{sin}\left(\frac{\mathrm{2}\pi{n}}{\mathrm{2}{n}+\mathrm{1}}\right)\:=\:\mathrm{sin}\left(\pi−\frac{\pi}{\mathrm{2}{n}+\mathrm{1}}\right)\:=\:\mathrm{sin}\left(\frac{\pi}{\mathrm{2}{n}+\mathrm{1}}\right) \\ $$$$\Rightarrow\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}\mathrm{cos}\left(\frac{{k}\pi}{\mathrm{2}{n}+\mathrm{1}}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}^{{n}} } \\ $$$$ \\ $$$$ \\ $$
