Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 115095 by aurpeyz last updated on 23/Sep/20

Answered by Dwaipayan Shikari last updated on 23/Sep/20

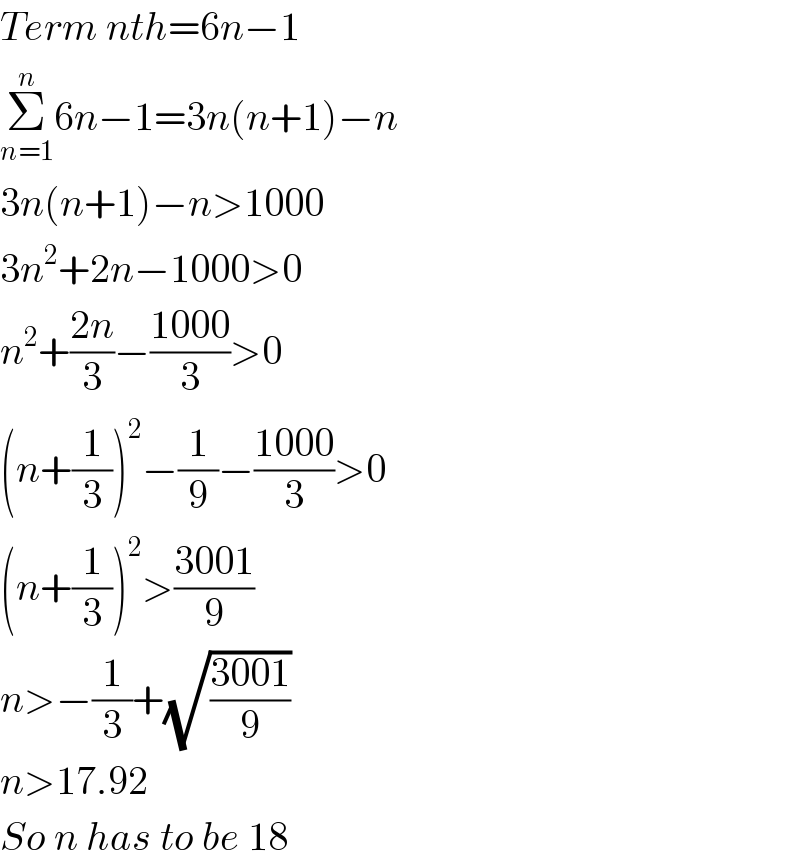
Term nth=6n−1 Σ_(n=1) ^n 6n−1=3n(n+1)−n 3n(n+1)−n>1000 3n^2 +2n−1000>0 n^2 +((2n)/3)−((1000)/3)>0 (n+(1/3))^2 −(1/9)−((1000)/3)>0 (n+(1/3))^2 >((3001)/9) n>−(1/3)+(√((3001)/9)) n>17.92 So n has to be 18

$${Term}\:{nth}=\mathrm{6}{n}−\mathrm{1} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{6}{n}−\mathrm{1}=\mathrm{3}{n}\left({n}+\mathrm{1}\right)−{n} \\ $$$$\mathrm{3}{n}\left({n}+\mathrm{1}\right)−{n}>\mathrm{1000} \\ $$$$\mathrm{3}{n}^{\mathrm{2}} +\mathrm{2}{n}−\mathrm{1000}>\mathrm{0} \\ $$$${n}^{\mathrm{2}} +\frac{\mathrm{2}{n}}{\mathrm{3}}−\frac{\mathrm{1000}}{\mathrm{3}}>\mathrm{0} \\ $$$$\left({n}+\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{9}}−\frac{\mathrm{1000}}{\mathrm{3}}>\mathrm{0} \\ $$$$\left({n}+\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} >\frac{\mathrm{3001}}{\mathrm{9}} \\ $$$${n}>−\frac{\mathrm{1}}{\mathrm{3}}+\sqrt{\frac{\mathrm{3001}}{\mathrm{9}}} \\ $$$${n}>\mathrm{17}.\mathrm{92} \\ $$$${So}\:{n}\:{has}\:{to}\:{be}\:\mathrm{18}\: \\ $$

Commented by aurpeyz last updated on 23/Sep/20

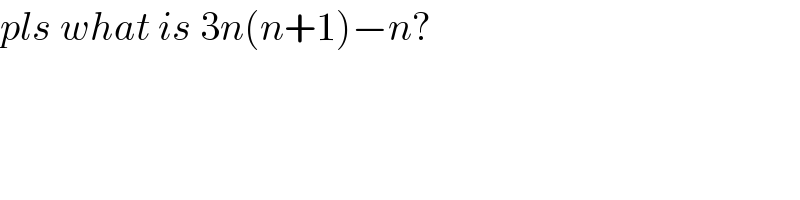
pls what is 3n(n+1)−n?

$${pls}\:{what}\:{is}\:\mathrm{3}{n}\left({n}+\mathrm{1}\right)−{n}? \\ $$

Commented by Dwaipayan Shikari last updated on 23/Sep/20

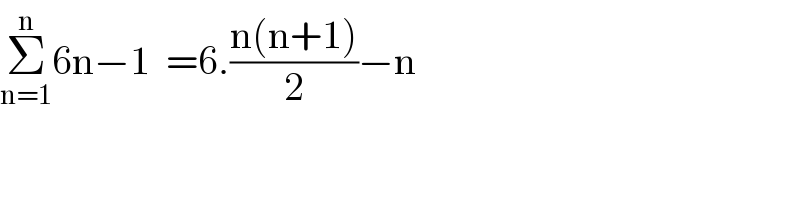
Σ_(n=1) ^n 6n−1 =6.((n(n+1))/2)−n

$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{6n}−\mathrm{1}\:\:=\mathrm{6}.\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{2}}−\mathrm{n} \\ $$

Answered by Aziztisffola last updated on 23/Sep/20

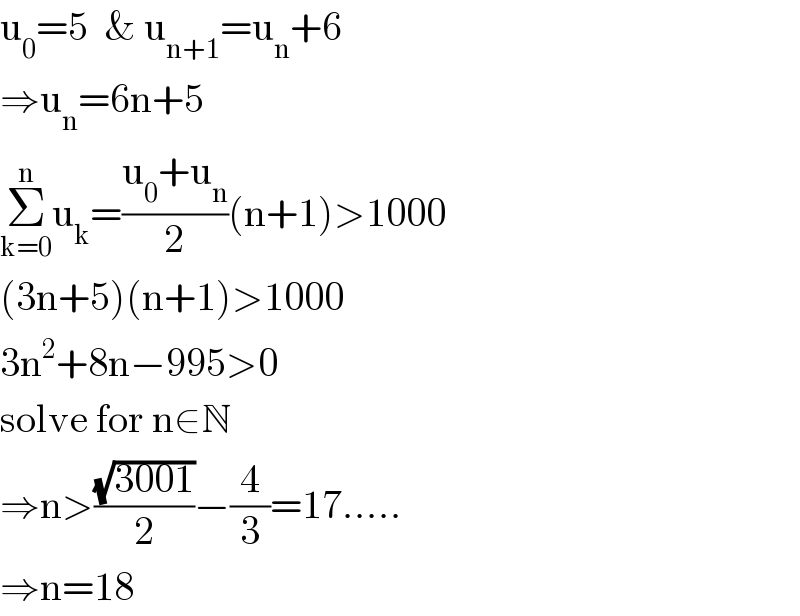
u_0 =5 & u_(n+1) =u_n +6 ⇒u_n =6n+5 Σ_(k=0) ^n u_k =((u_0 +u_n )/2)(n+1)>1000 (3n+5)(n+1)>1000 3n^2 +8n−995>0 solve for n∈N ⇒n>((√(3001))/2)−(4/3)=17..... ⇒n=18

$$\mathrm{u}_{\mathrm{0}} =\mathrm{5}\:\:\&\:\mathrm{u}_{\mathrm{n}+\mathrm{1}} =\mathrm{u}_{\mathrm{n}} +\mathrm{6} \\ $$$$\Rightarrow\mathrm{u}_{\mathrm{n}} =\mathrm{6n}+\mathrm{5} \\ $$$$\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{u}_{\mathrm{k}} =\frac{\mathrm{u}_{\mathrm{0}} +\mathrm{u}_{\mathrm{n}} }{\mathrm{2}}\left(\mathrm{n}+\mathrm{1}\right)>\mathrm{1000} \\ $$$$\left(\mathrm{3n}+\mathrm{5}\right)\left(\mathrm{n}+\mathrm{1}\right)>\mathrm{1000} \\ $$$$\mathrm{3n}^{\mathrm{2}} +\mathrm{8n}−\mathrm{995}>\mathrm{0} \\ $$$$\mathrm{solve}\:\mathrm{for}\:\mathrm{n}\in\mathbb{N} \\ $$$$\Rightarrow\mathrm{n}>\frac{\sqrt{\mathrm{3001}}}{\mathrm{2}}−\frac{\mathrm{4}}{\mathrm{3}}=\mathrm{17}..... \\ $$$$\Rightarrow\mathrm{n}=\mathrm{18} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com