
Question Number 115085 by Khalmohmmad last updated on 23/Sep/20
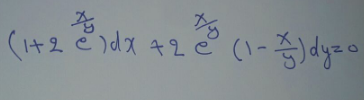
Commented by mohammad17 last updated on 23/Sep/20
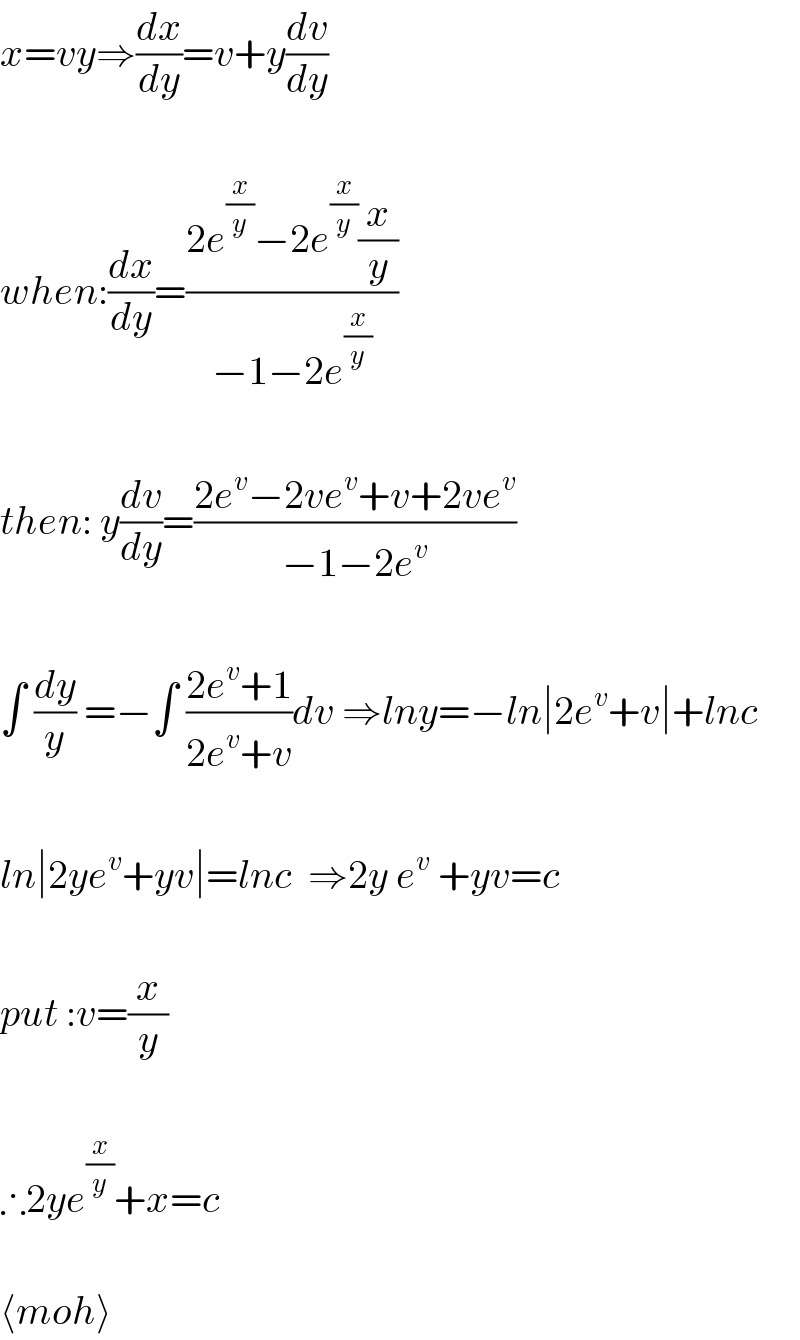
$${x}={vy}\Rightarrow\frac{{dx}}{{dy}}={v}+{y}\frac{{dv}}{{dy}} \\ $$$$ \\ $$$${when}:\frac{{dx}}{{dy}}=\frac{\mathrm{2}{e}^{\frac{{x}}{{y}}} −\mathrm{2}{e}^{\frac{{x}}{{y}}} \frac{{x}}{{y}}}{−\mathrm{1}−\mathrm{2}{e}^{\frac{{x}}{{y}}} } \\ $$$$ \\ $$$${then}:\:{y}\frac{{dv}}{{dy}}=\frac{\mathrm{2}{e}^{{v}} −\mathrm{2}{ve}^{{v}} +{v}+\mathrm{2}{ve}^{{v}} }{−\mathrm{1}−\mathrm{2}{e}^{{v}} } \\ $$$$ \\ $$$$\int\:\frac{{dy}}{{y}}\:=−\int\:\frac{\mathrm{2}{e}^{{v}} +\mathrm{1}}{\mathrm{2}{e}^{{v}} +{v}}{dv}\:\Rightarrow{lny}=−{ln}\mid\mathrm{2}{e}^{{v}} +{v}\mid+{lnc} \\ $$$$ \\ $$$${ln}\mid\mathrm{2}{ye}^{{v}} +{yv}\mid={lnc}\:\:\Rightarrow\mathrm{2}{y}\:{e}^{{v}} \:+{yv}={c} \\ $$$$ \\ $$$${put}\::{v}=\frac{{x}}{{y}} \\ $$$$ \\ $$$$\therefore\mathrm{2}{ye}^{\frac{{x}}{{y}}} +{x}={c} \\ $$$$ \\ $$$$\langle{moh}\rangle \\ $$
