
Question Number 114876 by mohammad17 last updated on 21/Sep/20

Commented by mohammad17 last updated on 21/Sep/20
$${plese}\:{sir}\:{help}\:{me}\:{please}\:? \\ $$
Answered by john santu last updated on 21/Sep/20
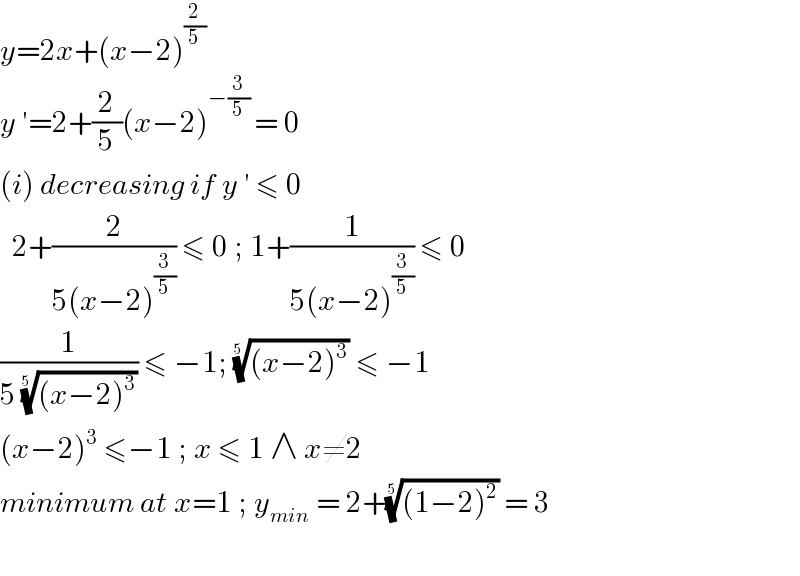
$${y}=\mathrm{2}{x}+\left({x}−\mathrm{2}\right)^{\frac{\mathrm{2}}{\mathrm{5}}} \\ $$$${y}\:'=\mathrm{2}+\frac{\mathrm{2}}{\mathrm{5}}\left({x}−\mathrm{2}\right)^{−\frac{\mathrm{3}}{\mathrm{5}}\:} =\:\mathrm{0} \\ $$$$\left({i}\right)\:{decreasing}\:{if}\:{y}\:'\:\leqslant\:\mathrm{0} \\ $$$$\:\:\mathrm{2}+\frac{\mathrm{2}}{\mathrm{5}\left({x}−\mathrm{2}\right)^{\frac{\mathrm{3}}{\mathrm{5}}} }\:\leqslant\:\mathrm{0}\:;\:\mathrm{1}+\frac{\mathrm{1}}{\mathrm{5}\left({x}−\mathrm{2}\right)^{\frac{\mathrm{3}}{\mathrm{5}}} }\:\leqslant\:\mathrm{0} \\ $$$$\frac{\mathrm{1}}{\mathrm{5}\:\sqrt[{\mathrm{5}\:}]{\left({x}−\mathrm{2}\right)^{\mathrm{3}} }}\:\leqslant\:−\mathrm{1};\:\sqrt[{\mathrm{5}\:}]{\left({x}−\mathrm{2}\right)^{\mathrm{3}} }\:\leqslant\:−\mathrm{1} \\ $$$$\left({x}−\mathrm{2}\right)^{\mathrm{3}} \:\leqslant−\mathrm{1}\:;\:{x}\:\leqslant\:\mathrm{1}\:\wedge\:{x}\neq\mathrm{2} \\ $$$${minimum}\:{at}\:{x}=\mathrm{1}\:;\:{y}_{{min}} \:=\:\mathrm{2}+\sqrt[{\mathrm{5}}]{\left(\mathrm{1}−\mathrm{2}\right)^{\mathrm{2}} }\:=\:\mathrm{3}\: \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 21/Sep/20
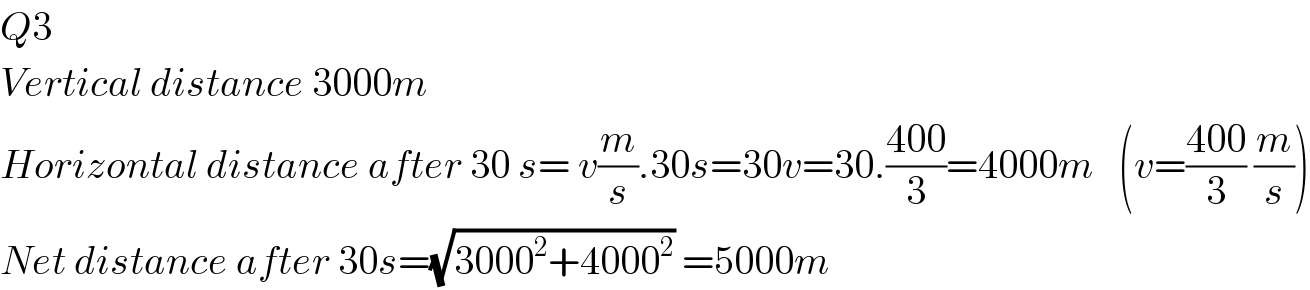
$${Q}\mathrm{3}\: \\ $$$${Vertical}\:{distance}\:\mathrm{3000}{m} \\ $$$${Horizontal}\:{distance}\:{after}\:\mathrm{30}\:{s}=\:{v}\frac{{m}}{{s}}.\mathrm{30}{s}=\mathrm{30}{v}=\mathrm{30}.\frac{\mathrm{400}}{\mathrm{3}}=\mathrm{4000}{m}\:\:\:\left({v}=\frac{\mathrm{400}}{\mathrm{3}}\:\frac{{m}}{{s}}\right) \\ $$$${Net}\:{distance}\:{after}\:\mathrm{30}{s}=\sqrt{\mathrm{3000}^{\mathrm{2}} +\mathrm{4000}^{\mathrm{2}} }\:=\mathrm{5000}{m} \\ $$
