
Question Number 114806 by Algoritm last updated on 21/Sep/20
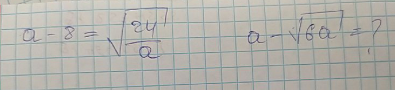
Answered by MJS_new last updated on 21/Sep/20
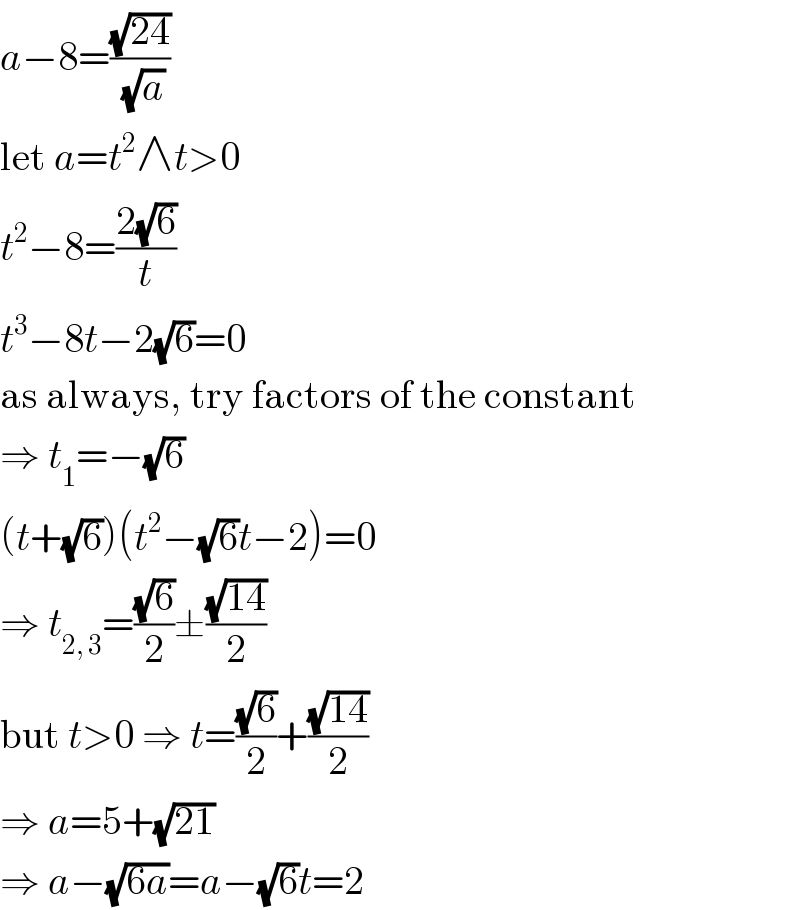
$${a}−\mathrm{8}=\frac{\sqrt{\mathrm{24}}}{\:\sqrt{{a}}} \\ $$$$\mathrm{let}\:{a}={t}^{\mathrm{2}} \wedge{t}>\mathrm{0} \\ $$$${t}^{\mathrm{2}} −\mathrm{8}=\frac{\mathrm{2}\sqrt{\mathrm{6}}}{{t}} \\ $$$${t}^{\mathrm{3}} −\mathrm{8}{t}−\mathrm{2}\sqrt{\mathrm{6}}=\mathrm{0} \\ $$$$\mathrm{as}\:\mathrm{always},\:\mathrm{try}\:\mathrm{factors}\:\mathrm{of}\:\mathrm{the}\:\mathrm{constant} \\ $$$$\Rightarrow\:{t}_{\mathrm{1}} =−\sqrt{\mathrm{6}} \\ $$$$\left({t}+\sqrt{\mathrm{6}}\right)\left({t}^{\mathrm{2}} −\sqrt{\mathrm{6}}{t}−\mathrm{2}\right)=\mathrm{0} \\ $$$$\Rightarrow\:{t}_{\mathrm{2},\:\mathrm{3}} =\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{14}}}{\mathrm{2}} \\ $$$$\mathrm{but}\:{t}>\mathrm{0}\:\Rightarrow\:{t}=\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}+\frac{\sqrt{\mathrm{14}}}{\mathrm{2}} \\ $$$$\Rightarrow\:{a}=\mathrm{5}+\sqrt{\mathrm{21}} \\ $$$$\Rightarrow\:{a}−\sqrt{\mathrm{6}{a}}={a}−\sqrt{\mathrm{6}}{t}=\mathrm{2} \\ $$
