Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 114796 by Algoritm last updated on 21/Sep/20

Answered by MJS_new last updated on 21/Sep/20

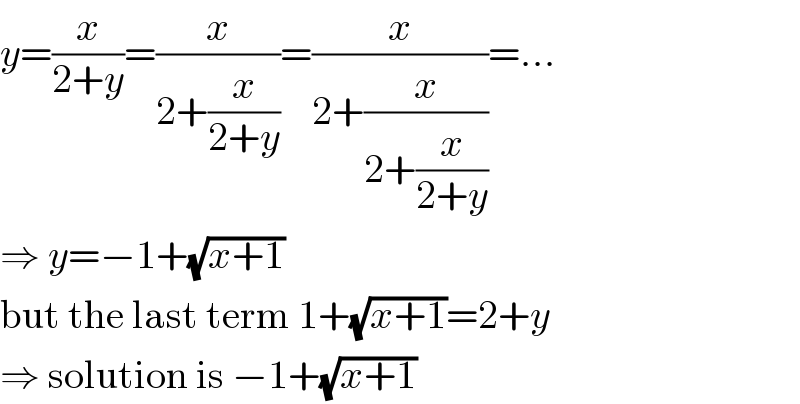
y=(x/(2+y))=(x/(2+(x/(2+y))))=(x/(2+(x/(2+(x/(2+y))))))=... ⇒ y=−1+(√(x+1)) but the last term 1+(√(x+1))=2+y ⇒ solution is −1+(√(x+1))

$${y}=\frac{{x}}{\mathrm{2}+{y}}=\frac{{x}}{\mathrm{2}+\frac{{x}}{\mathrm{2}+{y}}}=\frac{{x}}{\mathrm{2}+\frac{{x}}{\mathrm{2}+\frac{{x}}{\mathrm{2}+{y}}}}=... \\ $$$$\Rightarrow\:{y}=−\mathrm{1}+\sqrt{{x}+\mathrm{1}} \\ $$$$\mathrm{but}\:\mathrm{the}\:\mathrm{last}\:\mathrm{term}\:\mathrm{1}+\sqrt{{x}+\mathrm{1}}=\mathrm{2}+{y} \\ $$$$\Rightarrow\:\mathrm{solution}\:\mathrm{is}\:−\mathrm{1}+\sqrt{{x}+\mathrm{1}} \\ $$

Answered by PRITHWISH SEN 2 last updated on 21/Sep/20

the last term = 2+(x/(1+(√(x+1)))) = ((x+2+2(√(x+1)))/(1+(√(x+1)))) = ((((√(x+1))+1)^2 )/(((√(x+1))+1)) = (√(x+1)) +1 and the previous to the last term is = 2+(x/(1+(√(1+x)))) = last term ∴ the expression becomes = (x/( (√(x+1))+1)) = (√(x+1))−1

$$\mathrm{the}\:\mathrm{last}\:\mathrm{term}\:=\:\mathrm{2}+\frac{\mathrm{x}}{\mathrm{1}+\sqrt{\mathrm{x}+\mathrm{1}}}\:=\:\frac{\mathrm{x}+\mathrm{2}+\mathrm{2}\sqrt{\mathrm{x}+\mathrm{1}}}{\mathrm{1}+\sqrt{\mathrm{x}+\mathrm{1}}} \\ $$$$\:\:\:\:\:=\:\frac{\left(\sqrt{\mathrm{x}+\mathrm{1}}+\mathrm{1}\right)^{\mathrm{2}} }{\left(\sqrt{\mathrm{x}+\mathrm{1}}+\mathrm{1}\right.}\:=\:\sqrt{\mathrm{x}+\mathrm{1}}\:+\mathrm{1} \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{previous}\:\mathrm{to}\:\mathrm{the}\:\mathrm{last}\:\mathrm{term}\:\mathrm{is} \\ $$$$\:\:\:\:=\:\mathrm{2}+\frac{\mathrm{x}}{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{x}}}\:=\:\mathrm{last}\:\mathrm{term} \\ $$$$\therefore\:\mathrm{the}\:\mathrm{expression}\:\mathrm{becomes}\:=\:\frac{\mathrm{x}}{\:\sqrt{\mathrm{x}+\mathrm{1}}+\mathrm{1}}\:=\:\sqrt{\mathrm{x}+\mathrm{1}}−\mathrm{1} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com