
Question Number 11476 by tawa last updated on 26/Mar/17
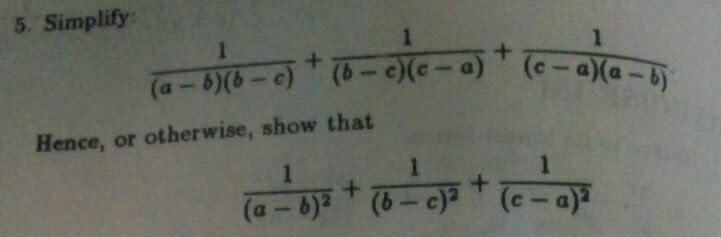
Answered by sandy_suhendra last updated on 27/Mar/17
![(1/((a−b)(b−c))) + (1/((b−c)(c−a))) + (1/((c−a)(a−b))) =((c−a+a−b+b−c)/((a−b)(b−c)(c−a))) = 0 (1/((a−b)^2 )) + (1/((b−c)^2 )) + (1/((c−a)^2 )) =[(1/((a−b))) + (1/((b−c))) + (1/((c−a)))]^2 − 2[(1/((a−b)(b−c)))+(1/((b−c)(c−a)))+(1/((c−a)(a−b)))] =[(1/((a−b)))+(1/((b−c)))+(1/((c−a)))]^2 − 2.0 =[(1/((a−b)))+(1/((b−c)))+(1/((c−a)))]^2](Q11505.png)
$$\frac{\mathrm{1}}{\left(\mathrm{a}−\mathrm{b}\right)\left(\mathrm{b}−\mathrm{c}\right)}\:+\:\frac{\mathrm{1}}{\left(\mathrm{b}−\mathrm{c}\right)\left(\mathrm{c}−\mathrm{a}\right)}\:+\:\frac{\mathrm{1}}{\left(\mathrm{c}−\mathrm{a}\right)\left(\mathrm{a}−\mathrm{b}\right)}\:\: \\ $$$$=\frac{\mathrm{c}−\mathrm{a}+\mathrm{a}−\mathrm{b}+\mathrm{b}−\mathrm{c}}{\left(\mathrm{a}−\mathrm{b}\right)\left(\mathrm{b}−\mathrm{c}\right)\left(\mathrm{c}−\mathrm{a}\right)}\:=\:\mathrm{0} \\ $$$$ \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{a}−\mathrm{b}\right)^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{\left(\mathrm{b}−\mathrm{c}\right)^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{\left(\mathrm{c}−\mathrm{a}\right)^{\mathrm{2}} } \\ $$$$=\left[\frac{\mathrm{1}}{\left(\mathrm{a}−\mathrm{b}\right)}\:+\:\frac{\mathrm{1}}{\left(\mathrm{b}−\mathrm{c}\right)}\:+\:\frac{\mathrm{1}}{\left(\mathrm{c}−\mathrm{a}\right)}\right]^{\mathrm{2}} −\:\mathrm{2}\left[\frac{\mathrm{1}}{\left(\mathrm{a}−\mathrm{b}\right)\left(\mathrm{b}−\mathrm{c}\right)}+\frac{\mathrm{1}}{\left(\mathrm{b}−\mathrm{c}\right)\left(\mathrm{c}−\mathrm{a}\right)}+\frac{\mathrm{1}}{\left(\mathrm{c}−\mathrm{a}\right)\left(\mathrm{a}−\mathrm{b}\right)}\right]\:\:\: \\ $$$$=\left[\frac{\mathrm{1}}{\left(\mathrm{a}−\mathrm{b}\right)}+\frac{\mathrm{1}}{\left(\mathrm{b}−\mathrm{c}\right)}+\frac{\mathrm{1}}{\left(\mathrm{c}−\mathrm{a}\right)}\right]^{\mathrm{2}} −\:\mathrm{2}.\mathrm{0} \\ $$$$=\left[\frac{\mathrm{1}}{\left(\mathrm{a}−\mathrm{b}\right)}+\frac{\mathrm{1}}{\left(\mathrm{b}−\mathrm{c}\right)}+\frac{\mathrm{1}}{\left(\mathrm{c}−\mathrm{a}\right)}\right]^{\mathrm{2}} \\ $$
Commented by tawa last updated on 27/Mar/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
