
Question Number 114654 by mohammad17 last updated on 20/Sep/20

Commented by mohammad17 last updated on 20/Sep/20

$${help}\:{me}\:{sir} \\ $$
Commented by mohammad17 last updated on 20/Sep/20
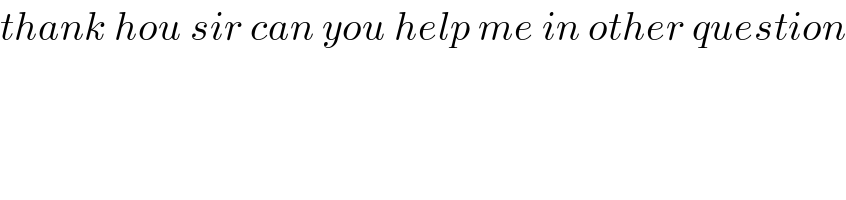
$${thank}\:{hou}\:{sir}\:{can}\:{you}\:{help}\:{me}\:{in}\:{other}\:{question} \\ $$
Answered by bobhans last updated on 20/Sep/20
![[2] x=acos^3 θ ⇒(dx/dθ) = −3acos^2 θ sin θ y=asin^3 θ⇒(dy/dθ) = 3asin^2 θ cos θ (dy/dx) = (dy/dθ) × (dθ/dx) = ((3asin^2 θ cos θ)/(−3acos^2 θ sin θ)) (dy/dx) = −((sin θ)/(cos θ)) = −tan θ (√(1+((dy/dx))^2 )) = (√(1+tan^2 θ)) = sec θ](Q114658.png)
$$\left[\mathrm{2}\right]\:{x}={a}\mathrm{cos}^{\mathrm{3}} \:\theta\:\Rightarrow\frac{{dx}}{{d}\theta}\:=\:−\mathrm{3}{a}\mathrm{cos}\:^{\mathrm{2}} \theta\:\mathrm{sin}\:\theta\: \\ $$$$\:\:\:\:\:\:\:{y}={a}\mathrm{sin}\:^{\mathrm{3}} \theta\Rightarrow\frac{{dy}}{{d}\theta}\:=\:\mathrm{3}{a}\mathrm{sin}\:^{\mathrm{2}} \theta\:\mathrm{cos}\:\theta \\ $$$$\:\:\:\:\:\:\:\frac{{dy}}{{dx}}\:=\:\frac{{dy}}{{d}\theta}\:×\:\frac{{d}\theta}{{dx}}\:=\:\frac{\mathrm{3}{a}\mathrm{sin}\:^{\mathrm{2}} \theta\:\mathrm{cos}\:\theta}{−\mathrm{3}{a}\mathrm{cos}\:^{\mathrm{2}} \theta\:\mathrm{sin}\:\theta} \\ $$$$\:\:\:\:\:\:\:\frac{{dy}}{{dx}}\:=\:−\frac{\mathrm{sin}\:\theta}{\mathrm{cos}\:\theta}\:=\:−\mathrm{tan}\:\theta \\ $$$$\:\:\:\:\:\sqrt{\mathrm{1}+\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} }\:=\:\sqrt{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \theta}\:=\:\mathrm{sec}\:\theta \\ $$
Answered by Dwaipayan Shikari last updated on 20/Sep/20
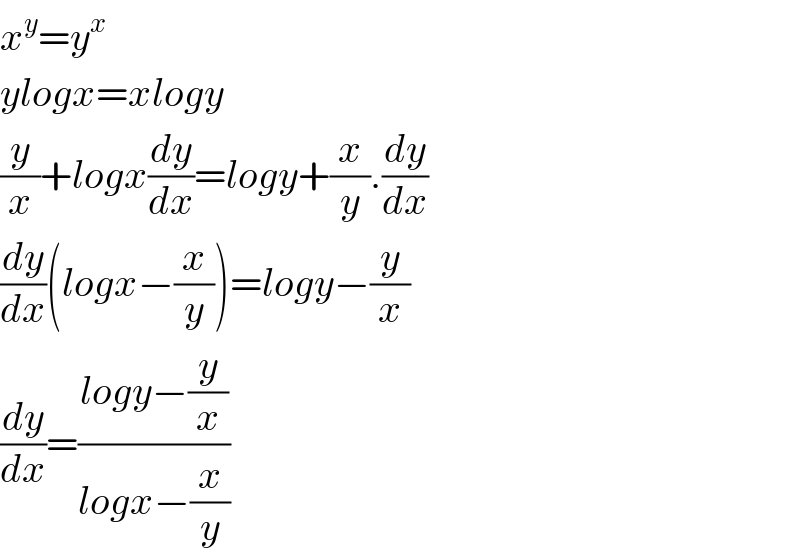
$${x}^{{y}} ={y}^{{x}} \\ $$$${ylogx}={xlogy} \\ $$$$\frac{{y}}{{x}}+{logx}\frac{{dy}}{{dx}}={logy}+\frac{{x}}{{y}}.\frac{{dy}}{{dx}} \\ $$$$\frac{{dy}}{{dx}}\left({logx}−\frac{{x}}{{y}}\right)={logy}−\frac{{y}}{{x}} \\ $$$$\frac{{dy}}{{dx}}=\frac{{logy}−\frac{{y}}{{x}}}{{logx}−\frac{{x}}{{y}}} \\ $$
