
Question Number 114475 by Rio Michael last updated on 19/Sep/20
Commented by Rio Michael last updated on 19/Sep/20

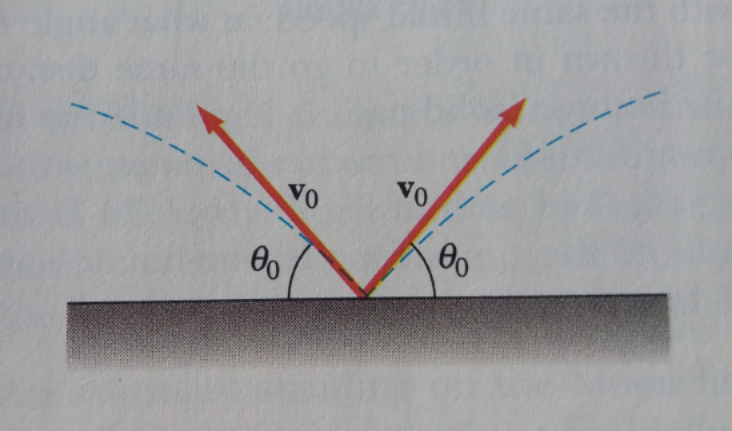
$$\mathrm{suppose}\:\mathrm{that}\:\mathrm{two}\:\mathrm{rocks}\:\mathrm{are}\:\mathrm{thrown}\:\mathrm{from} \\ $$$$\mathrm{thesame}\:\mathrm{point}\:\mathrm{at}\:\mathrm{the}\:\mathrm{same}\:\mathrm{moment}\:\mathrm{as}\:\mathrm{in} \\ $$$$\mathrm{the}\:\mathrm{figure}\:\mathrm{above}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{distance}\:\mathrm{between} \\ $$$$\mathrm{them}\:\mathrm{as}\:\mathrm{a}\:\mathrm{function}\:\mathrm{of}\:\mathrm{time}.\:\mathrm{Assume}\:\mathrm{that} \\ $$$${v}_{\mathrm{0}} \:\mathrm{and}\:\theta_{\mathrm{0}} \:\mathrm{are}\:\mathrm{given}. \\ $$
Commented by Dwaipayan Shikari last updated on 19/Sep/20

$${In}\:{t}_{\mathrm{1}} \:{time}\:{A}\:{particle}\:{will}\:{cross}\: \\ $$$${S}_{{y}} ={v}_{\mathrm{0}} {sin}\theta{t}_{\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}}{gt}_{\mathrm{1}} ^{\mathrm{2}} \:\:\:\:\left({upward}\right) \\ $$$${B}\:{particle}\:{goes}\:{S}_{{y}} '={v}_{\mathrm{0}} {sin}\theta{t}_{\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}}{gt}_{\mathrm{1}} ^{\mathrm{2}} \\ $$$${S}_{{y}} −{S}_{{y}} '=\mathrm{0} \\ $$$${In}\:{t}_{\mathrm{1}} \:{A}\:{particle}\:{goes}\:\left({v}_{\mathrm{0}} {cos}\theta_{\mathrm{0}} \right){t}_{\mathrm{1}} \:\:{toward}\:+{x}\:{direction} \\ $$$${B}\:{particle}\:{goes}\:\left({v}_{\mathrm{0}} {cos}\theta_{\mathrm{0}} \right){t}_{\mathrm{1}} \:{in}\:−{x}\:{direction} \\ $$$${Relative}\:{distance}\:{S}_{{x}} =\mathrm{2}{v}_{\mathrm{0}} {cos}\theta_{\mathrm{0}} {t}_{\mathrm{1}} \\ $$$$\sqrt{{S}_{{x}} ^{\mathrm{2}} +\left({S}_{{y}} −{S}_{{y}} '\right)^{\mathrm{2}} }\:\:=\mathrm{2}{v}_{\mathrm{0}} {cos}\theta_{\mathrm{0}} {t}_{\mathrm{1}} \\ $$
Commented by Rio Michael last updated on 19/Sep/20

$$\mathrm{thanks} \\ $$
Commented by Dwaipayan Shikari last updated on 19/Sep/20
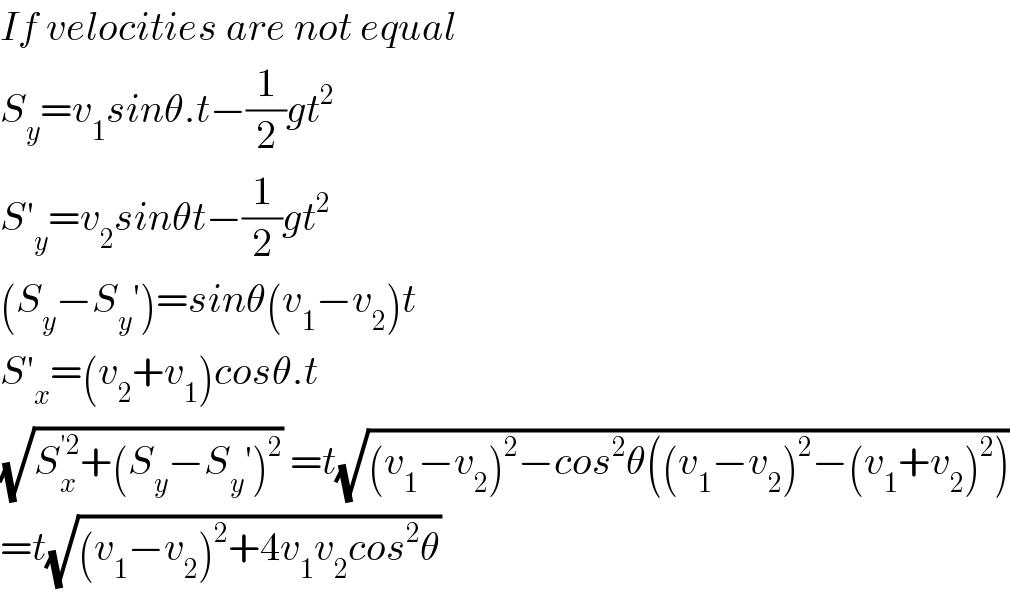
$${If}\:{velocities}\:{are}\:{not}\:{equal} \\ $$$${S}_{{y}} ={v}_{\mathrm{1}} {sin}\theta.{t}−\frac{\mathrm{1}}{\mathrm{2}}{gt}^{\mathrm{2}} \\ $$$${S}'_{{y}} ={v}_{\mathrm{2}} {sin}\theta{t}−\frac{\mathrm{1}}{\mathrm{2}}{gt}^{\mathrm{2}} \\ $$$$\left({S}_{{y}} −{S}_{{y}} '\right)={sin}\theta\left({v}_{\mathrm{1}} −{v}_{\mathrm{2}} \right){t} \\ $$$${S}'_{{x}} =\left({v}_{\mathrm{2}} +{v}_{\mathrm{1}} \right){cos}\theta.{t} \\ $$$$\sqrt{{S}_{{x}} ^{'\mathrm{2}} +\left({S}_{{y}} −{S}_{{y}} '\right)^{\mathrm{2}} }\:={t}\sqrt{\left({v}_{\mathrm{1}} −{v}_{\mathrm{2}} \right)^{\mathrm{2}} −{cos}^{\mathrm{2}} \theta\left(\left({v}_{\mathrm{1}} −{v}_{\mathrm{2}} \right)^{\mathrm{2}} −\left({v}_{\mathrm{1}} +{v}_{\mathrm{2}} \right)^{\mathrm{2}} \right)} \\ $$$$={t}\sqrt{\left({v}_{\mathrm{1}} −{v}_{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{4}{v}_{\mathrm{1}} {v}_{\mathrm{2}} {cos}^{\mathrm{2}} \theta} \\ $$
Commented by Rio Michael last updated on 19/Sep/20

$$\mathrm{thanks}\:\mathrm{for}\:\mathrm{the}\:\mathrm{extra} \\ $$
