
Question Number 113771 by mohammad17 last updated on 15/Sep/20

Answered by Dwaipayan Shikari last updated on 15/Sep/20
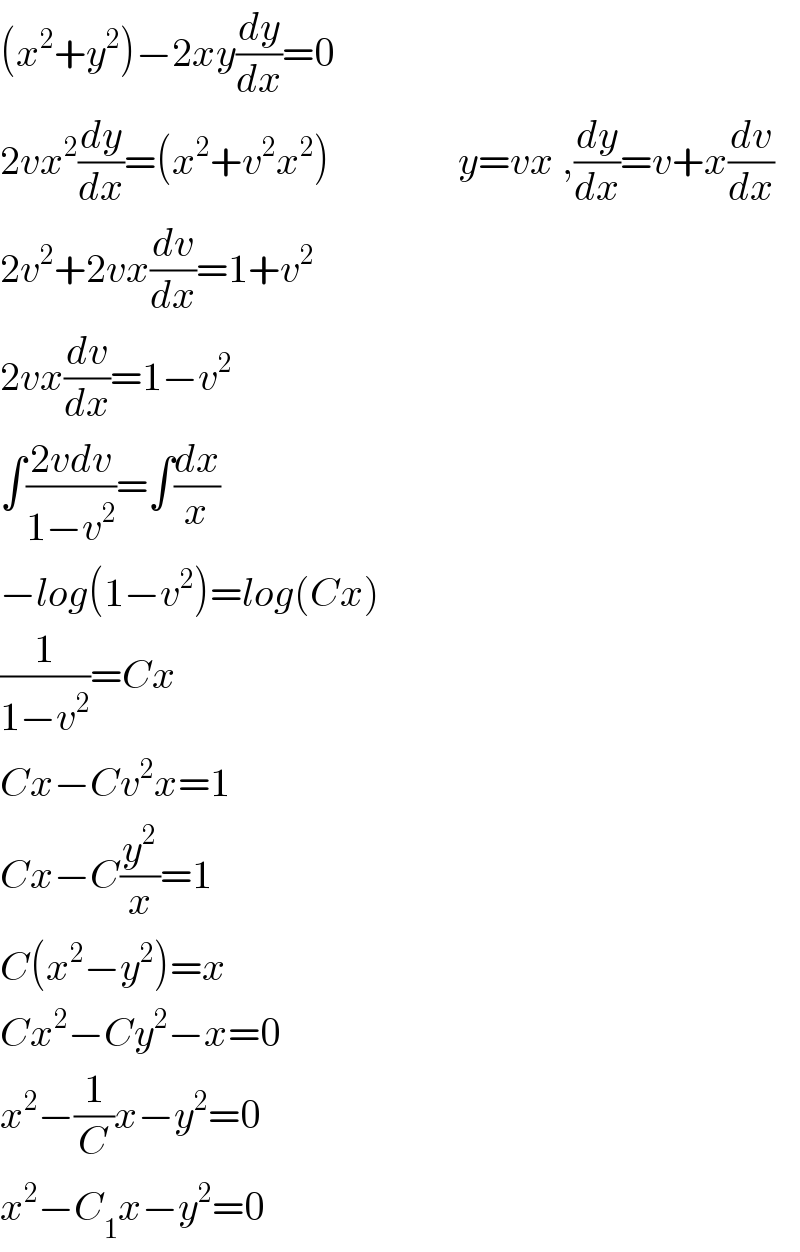
$$\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)−\mathrm{2}{xy}\frac{{dy}}{{dx}}=\mathrm{0} \\ $$$$\mathrm{2}{vx}^{\mathrm{2}} \frac{{dy}}{{dx}}=\left({x}^{\mathrm{2}} +{v}^{\mathrm{2}} {x}^{\mathrm{2}} \right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{y}={vx}\:,\frac{{dy}}{{dx}}={v}+{x}\frac{{dv}}{{dx}} \\ $$$$\mathrm{2}{v}^{\mathrm{2}} +\mathrm{2}{vx}\frac{{dv}}{{dx}}=\mathrm{1}+{v}^{\mathrm{2}} \\ $$$$\mathrm{2}{vx}\frac{{dv}}{{dx}}=\mathrm{1}−{v}^{\mathrm{2}} \\ $$$$\int\frac{\mathrm{2}{vdv}}{\mathrm{1}−{v}^{\mathrm{2}} }=\int\frac{{dx}}{{x}} \\ $$$$−{log}\left(\mathrm{1}−{v}^{\mathrm{2}} \right)={log}\left({Cx}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{1}−{v}^{\mathrm{2}} }={Cx} \\ $$$${Cx}−{Cv}^{\mathrm{2}} {x}=\mathrm{1} \\ $$$${Cx}−{C}\frac{{y}^{\mathrm{2}} }{{x}}=\mathrm{1} \\ $$$${C}\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)={x} \\ $$$${Cx}^{\mathrm{2}} −{Cy}^{\mathrm{2}} −{x}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} −\frac{\mathrm{1}}{{C}}{x}−{y}^{\mathrm{2}} =\mathrm{0} \\ $$$${x}^{\mathrm{2}} −{C}_{\mathrm{1}} {x}−{y}^{\mathrm{2}} =\mathrm{0} \\ $$
