
Question Number 113668 by mohammad17 last updated on 14/Sep/20

Answered by john santu last updated on 14/Sep/20
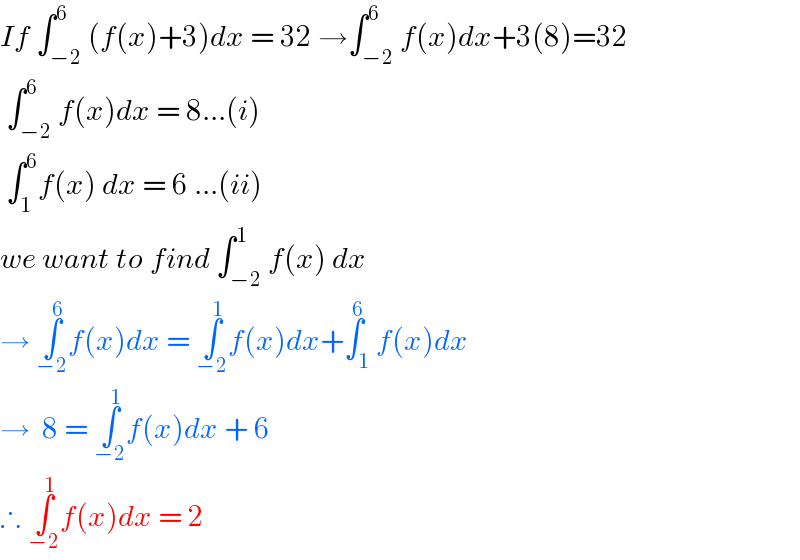
$${If}\:\int_{−\mathrm{2}} ^{\mathrm{6}} \left({f}\left({x}\right)+\mathrm{3}\right){dx}\:=\:\mathrm{32}\:\rightarrow\int_{−\mathrm{2}} ^{\mathrm{6}} {f}\left({x}\right){dx}+\mathrm{3}\left(\mathrm{8}\right)=\mathrm{32} \\ $$$$\:\int_{−\mathrm{2}} ^{\mathrm{6}} {f}\left({x}\right){dx}\:=\:\mathrm{8}...\left({i}\right) \\ $$$$\:\int_{\mathrm{1}} ^{\mathrm{6}} {f}\left({x}\right)\:{dx}\:=\:\mathrm{6}\:...\left({ii}\right) \\ $$$${we}\:{want}\:{to}\:{find}\:\int_{−\mathrm{2}} ^{\mathrm{1}} {f}\left({x}\right)\:{dx} \\ $$$$\rightarrow\:\underset{−\mathrm{2}} {\overset{\mathrm{6}} {\int}}{f}\left({x}\right){dx}\:=\:\underset{−\mathrm{2}} {\overset{\mathrm{1}} {\int}}{f}\left({x}\right){dx}+\overset{\mathrm{6}} {\int}_{\mathrm{1}} {f}\left({x}\right){dx} \\ $$$$\rightarrow\:\:\mathrm{8}\:=\:\underset{−\mathrm{2}} {\overset{\mathrm{1}} {\int}}{f}\left({x}\right){dx}\:+\:\mathrm{6}\: \\ $$$$\therefore\:\underset{−\mathrm{2}} {\overset{\mathrm{1}} {\int}}{f}\left({x}\right){dx}\:=\:\mathrm{2} \\ $$
Commented by mohammad17 last updated on 14/Sep/20
$${thank}\:{you}\:{sir}\:{very}\:{thank}\:{you} \\ $$
