
Question Number 113565 by bemath last updated on 14/Sep/20
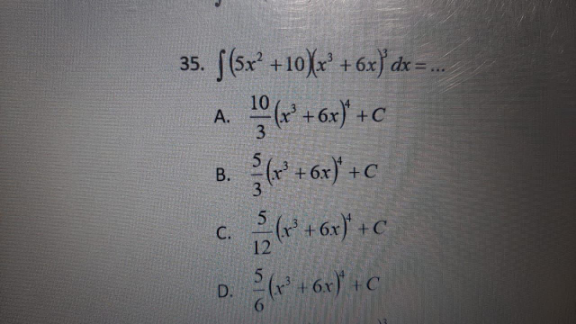
Answered by bobhans last updated on 14/Sep/20
![∫(5x^2 +10)(x^3 +6x)^3 dx = ∫5(x^2 +2)(x^3 +6x)^3 dx= [ u=x^3 +6x⇒du=3x^2 +6 dx ] ∫ 5(u)^3 ((1/3)du) = (5/3)∫ u^3 du = (5/(12))(x^3 +6x)^4 +c](Q113570.png)
$$\int\left(\mathrm{5x}^{\mathrm{2}} +\mathrm{10}\right)\left(\mathrm{x}^{\mathrm{3}} +\mathrm{6x}\right)^{\mathrm{3}} \mathrm{dx}\:= \\ $$$$\int\mathrm{5}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)\left(\mathrm{x}^{\mathrm{3}} +\mathrm{6x}\right)^{\mathrm{3}} \mathrm{dx}= \\ $$$$\left[\:\mathrm{u}=\mathrm{x}^{\mathrm{3}} +\mathrm{6x}\Rightarrow\mathrm{du}=\mathrm{3x}^{\mathrm{2}} +\mathrm{6}\:\mathrm{dx}\:\right] \\ $$$$\int\:\mathrm{5}\left(\mathrm{u}\right)^{\mathrm{3}} \left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{du}\right)\:=\:\frac{\mathrm{5}}{\mathrm{3}}\int\:\mathrm{u}^{\mathrm{3}} \:\mathrm{du}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{5}}{\mathrm{12}}\left(\mathrm{x}^{\mathrm{3}} +\mathrm{6x}\right)^{\mathrm{4}} +\mathrm{c} \\ $$
