
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 113486 by mr W last updated on 13/Sep/20
Commented by mr W last updated on 13/Sep/20

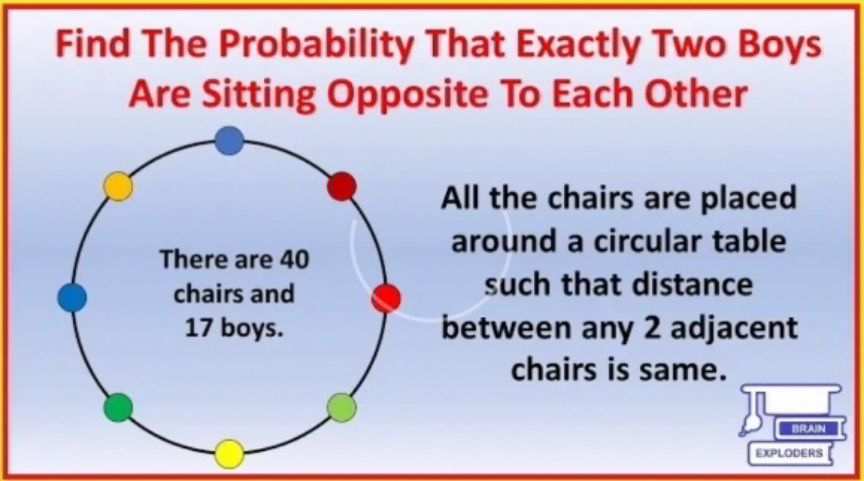
$${Repost}\:{Q}\mathrm{112509} \\ $$
Answered by mr W last updated on 13/Sep/20

$$\mathrm{40}\:{chairs}\:{build}\:\mathrm{20}\:{pairs}\:{with}\:{opposite} \\ $$$${chairs}. \\ $$$$ \\ $$$${for}\:\mathrm{17}\:{boys}\:{to}\:{take}\:{the}\:\mathrm{40}\:{chairs}\:{on} \\ $$$${the}\:{table}\:{there}\:{are}\:{totally}\:{P}_{\mathrm{17}−\mathrm{1}} ^{\mathrm{40}−\mathrm{1}} \:{ways}. \\ $$$$ \\ $$$${to}\:{select}\:{two}\:{boys}\:{who}\:{sit}\:{opposite} \\ $$$${there}\:{are}\:{C}_{\mathrm{2}} ^{\mathrm{17}} \:{ways}. \\ $$$${to}\:{select}\:\mathrm{15}\:{from}\:\mathrm{19}\:{chair}\:{pairs}\:{there} \\ $$$${are}\:{C}_{\mathrm{15}} ^{\mathrm{19}} \:{ways}.\:{to}\:{arrange}\:{the}\:\mathrm{15}\:{boys} \\ $$$${in}\:{these}\:{chairs}\:{there}\:{are}\:\mathrm{15}!×\mathrm{2}^{\mathrm{15}} \\ $$$${ways}. \\ $$$${totally}\:{C}_{\mathrm{2}} ^{\mathrm{17}} ×{C}_{\mathrm{15}} ^{\mathrm{19}} ×\mathrm{15}!×\mathrm{2}^{\mathrm{15}} . \\ $$$$ \\ $$$${p}=\frac{{C}_{\mathrm{2}} ^{\mathrm{17}} ×{C}_{\mathrm{15}} ^{\mathrm{19}} ×\mathrm{15}!×\mathrm{2}^{\mathrm{15}} }{{P}_{\mathrm{16}} ^{\mathrm{39}} }=\mathrm{2}.\mathrm{8627\%} \\ $$
Commented by I want to learn more last updated on 13/Sep/20
$$\mathrm{Thanks}\:\mathrm{sir},\:\:\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate} \\ $$
Commented by I want to learn more last updated on 14/Sep/20
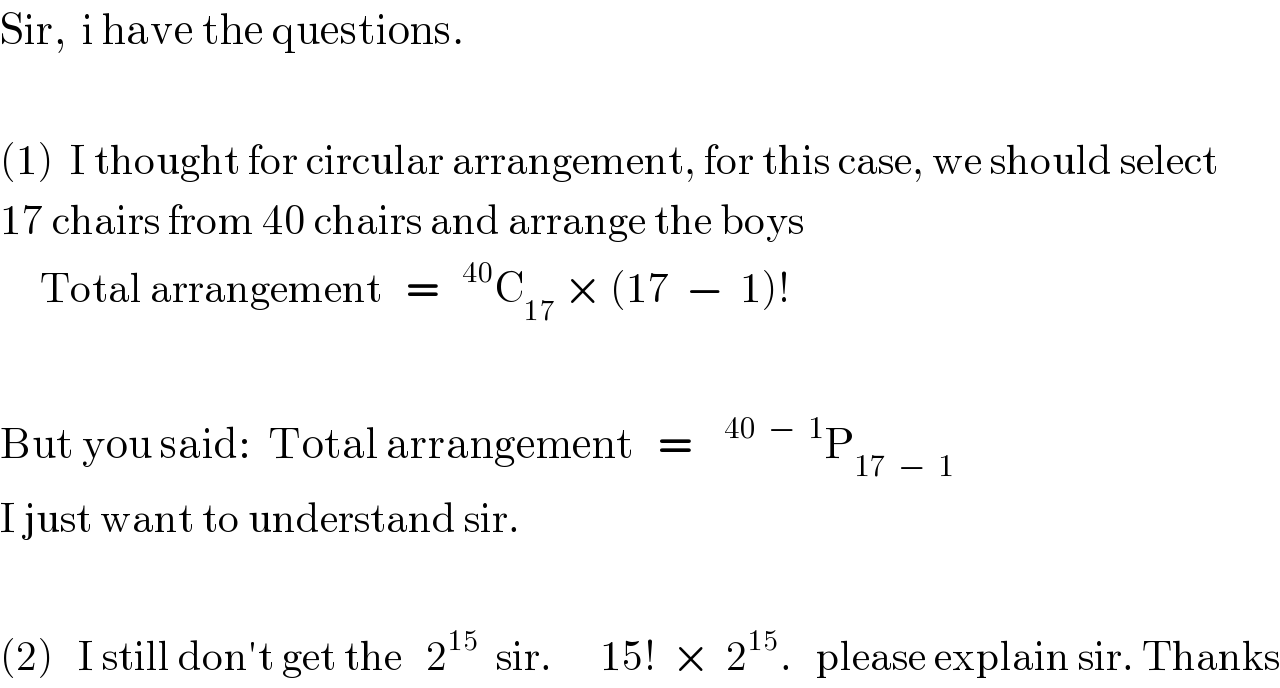
$$\mathrm{Sir},\:\:\mathrm{i}\:\mathrm{have}\:\mathrm{the}\:\mathrm{questions}. \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\:\:\mathrm{I}\:\mathrm{thought}\:\mathrm{for}\:\mathrm{circular}\:\mathrm{arrangement},\:\mathrm{for}\:\mathrm{this}\:\mathrm{case},\:\mathrm{we}\:\mathrm{should}\:\mathrm{select} \\ $$$$\mathrm{17}\:\mathrm{chairs}\:\mathrm{from}\:\mathrm{40}\:\mathrm{chairs}\:\mathrm{and}\:\mathrm{arrange}\:\mathrm{the}\:\mathrm{boys} \\ $$$$\:\:\:\:\:\mathrm{Total}\:\mathrm{arrangement}\:\:\:=\:\:\:^{\mathrm{40}} \mathrm{C}_{\mathrm{17}} \:×\:\left(\mathrm{17}\:\:−\:\:\mathrm{1}\right)! \\ $$$$ \\ $$$$\mathrm{But}\:\mathrm{you}\:\mathrm{said}:\:\:\mathrm{Total}\:\mathrm{arrangement}\:\:\:=\:\:\:\:^{\mathrm{40}\:\:−\:\:\mathrm{1}} \mathrm{P}_{\mathrm{17}\:\:−\:\:\mathrm{1}} \\ $$$$\mathrm{I}\:\mathrm{just}\:\mathrm{want}\:\mathrm{to}\:\mathrm{understand}\:\mathrm{sir}. \\ $$$$ \\ $$$$\left(\mathrm{2}\right)\:\:\:\mathrm{I}\:\mathrm{still}\:\mathrm{don}'\mathrm{t}\:\mathrm{get}\:\mathrm{the}\:\:\:\mathrm{2}^{\mathrm{15}} \:\:\mathrm{sir}.\:\:\:\:\:\:\mathrm{15}!\:\:×\:\:\mathrm{2}^{\mathrm{15}} .\:\:\:\mathrm{please}\:\mathrm{explain}\:\mathrm{sir}.\:\mathrm{Thanks} \\ $$
Commented by mr W last updated on 14/Sep/20

$$\left(\mathrm{2}\right) \\ $$$${in}\:{the}\:\mathrm{15}\:{pairs}\:{of}\:{seats}\:{each}\:{boy}\:{can} \\ $$$${select}\:{one}\:{of}\:{the}\:{two}\:{seats},\:{so}\:{totally} \\ $$$${there}\:{are}\:\mathrm{2}^{\mathrm{15}} \:{different}\:{ways}. \\ $$
Commented by mr W last updated on 14/Sep/20

$$\left(\mathrm{1}\right) \\ $$$${you}\:{can}\:{read}\:{a}\:{text}\:{book}\:{about}\:{circular} \\ $$$${arrangement}. \\ $$$${my}\:{way}\:{to}\:{understand}: \\ $$$${in}\:{a}\:{circular}\:{arrangement}\:{it}\:{doesn}'{t} \\ $$$${matter}\:{where}\:{the}\:{arrangement} \\ $$$${beginns}.\:{so}\:{we}\:{can}\:{fix}\:{a}\:{boy}\:{in}\:{a}\:{seat}. \\ $$$${we}\:{only}\:{need}\:{to}\:{determine}\:{in}\:{how} \\ $$$${many}\:{ways}\:{we}\:{can}\:{arrange}\:{the}\: \\ $$$${remaining}\:\mathrm{16}\:{boys}\:{in}\:{the}\:{remaining} \\ $$$$\mathrm{39}\:{seats},\:{that}\:{is}\:{P}_{\mathrm{16}} ^{\mathrm{39}} . \\ $$
Commented by I want to learn more last updated on 14/Sep/20

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{understand}\:\mathrm{now} \\ $$
