
Question Number 113455 by AbhishekBasnet last updated on 13/Sep/20

Commented by som(math1967) last updated on 13/Sep/20
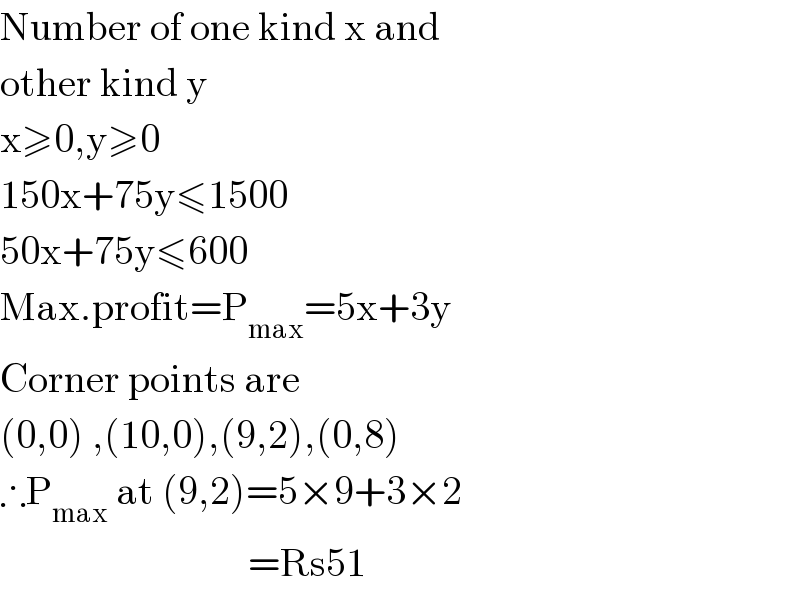
$$\mathrm{Number}\:\mathrm{of}\:\mathrm{one}\:\mathrm{kind}\:\mathrm{x}\:\mathrm{and} \\ $$$$\mathrm{other}\:\mathrm{kind}\:\mathrm{y} \\ $$$$\mathrm{x}\geqslant\mathrm{0},\mathrm{y}\geqslant\mathrm{0} \\ $$$$\mathrm{150x}+\mathrm{75y}\leqslant\mathrm{1500} \\ $$$$\mathrm{50x}+\mathrm{75y}\leqslant\mathrm{600} \\ $$$$\mathrm{Max}.\mathrm{profit}=\mathrm{P}_{\mathrm{max}} =\mathrm{5x}+\mathrm{3y} \\ $$$$\mathrm{Corner}\:\mathrm{points}\:\mathrm{are} \\ $$$$\left(\mathrm{0},\mathrm{0}\right)\:,\left(\mathrm{10},\mathrm{0}\right),\left(\mathrm{9},\mathrm{2}\right),\left(\mathrm{0},\mathrm{8}\right) \\ $$$$\therefore\mathrm{P}_{\mathrm{max}} \:\mathrm{at}\:\left(\mathrm{9},\mathrm{2}\right)=\mathrm{5}×\mathrm{9}+\mathrm{3}×\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{Rs51} \\ $$
Answered by 1549442205PVT last updated on 13/Sep/20

$$\mathrm{Suppose}\:\mathrm{first}\:\mathrm{kind}\:\mathrm{of}\:\mathrm{cake}\:\mathrm{is}\:\mathrm{made}\:\mathrm{x} \\ $$$$\mathrm{boxes}\:\mathrm{and}\:\mathrm{second}\:\mathrm{kind}\:\mathrm{of}\:\mathrm{cakes}\:\mathrm{is} \\ $$$$\mathrm{made}\:\mathrm{y}\:\mathrm{boxes}.\mathrm{From}\:\mathrm{the}\:\mathrm{hypothesis}\: \\ $$$$\mathrm{we}\:\mathrm{has}\:\mathrm{the}\:\mathrm{system}\:: \\ $$$$\begin{cases}{\mathrm{150x}+\mathrm{75y}=\mathrm{1500}\left(\mathrm{1}\right)}\\{\mathrm{50x}+\mathrm{75y}=\mathrm{600}\left(\mathrm{2}\right)}\end{cases} \\ $$$$\mathrm{Substracting}\:\mathrm{two}\:\mathrm{equations}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{100x}=\mathrm{900}\Rightarrow\mathrm{x}=\mathrm{9}.\mathrm{Replace}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{y}=\mathrm{2}.\mathrm{Then}\:\mathrm{the}\:\mathrm{profits}\:\mathrm{obtain}\:\mathrm{equal}\:\mathrm{to} \\ $$$$\mathrm{9}×\mathrm{5}+\mathrm{2}×\mathrm{3}=\mathrm{51}\:\left(\mathrm{Rs}\right) \\ $$$$\bullet\mathrm{If}\:\mathrm{made}\:\mathrm{10}\:\mathrm{boxes}\:\mathrm{of}\:\mathrm{first}\:\mathrm{kind}\:\mathrm{of}\:\mathrm{cakes} \\ $$$$\mathrm{then}\:\mathrm{the}\:\mathrm{second}\:\mathrm{kind}\:\mathrm{of}\:\mathrm{cakes}\:\mathrm{has}\:\mathrm{no} \\ $$$$\mathrm{boxes}\:\mathrm{because}\:\mathrm{10}×\mathrm{150}=\mathrm{1500gr}\:\mathrm{flour} \\ $$$$,\mathrm{so}\:\mathrm{has}\:\mathrm{no}\:\mathrm{flour}\:\mathrm{to}\:\mathrm{make}\:\mathrm{second}\:\mathrm{kind}\:\mathrm{of}\:\mathrm{cakes} \\ $$$$\bullet\mathrm{From}\:\mathrm{above}\:\mathrm{result}\:\mathrm{we}\:\mathrm{infer}\:\mathrm{a}+\mathrm{b}\leqslant\mathrm{11} \\ $$$$\mathrm{and}\:\mathrm{a}\leqslant\mathrm{9}\Rightarrow\mathrm{b}\leqslant\mathrm{11}−\mathrm{a} \\ $$$$\mathrm{The}\:\mathrm{profits}\:\mathrm{value}\:\mathrm{obtain}\:\mathrm{is} \\ $$$$\mathrm{M}=\mathrm{5a}+\mathrm{3b}\leqslant\mathrm{5a}+\mathrm{3}\left(\mathrm{11}−\mathrm{a}\right)=\mathrm{2a}+\mathrm{33} \\ $$$$\leqslant\mathrm{2}×\mathrm{9}+\mathrm{33}=\mathrm{51} \\ $$$$\mathrm{Thus},\mathrm{the}\:\mathrm{best}\:\mathrm{option}\:\mathrm{for}\:\mathrm{candy} \\ $$$$\mathrm{product}\:\mathrm{are}\:\mathrm{9}\:\mathrm{boxes}\:\mathrm{of}\:\mathrm{1}\:\mathrm{type}\:\mathrm{and}\:\mathrm{2} \\ $$$$\mathrm{boxes}\:\mathrm{of}\:\mathrm{2}\:\mathrm{type} \\ $$
