Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 112162 by 175mohamed last updated on 06/Sep/20

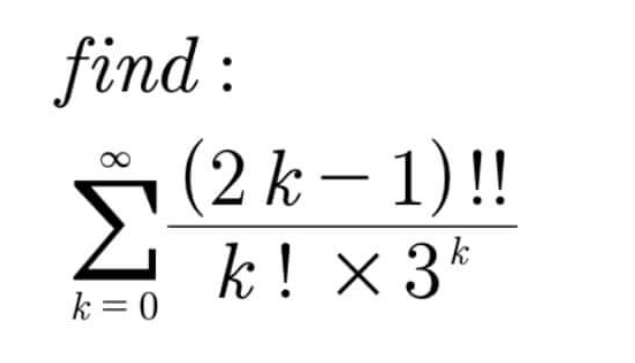
Commented by JDamian last updated on 06/Sep/20

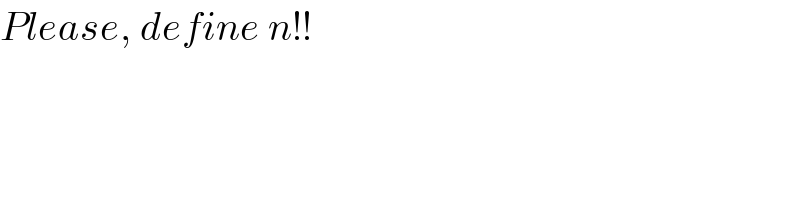
Please, define n!!

$${Please},\:{define}\:{n}!! \\ $$

Commented by mnjuly1970 last updated on 06/Sep/20

n!! (double factorial) if n=2k ⇒ (2k)!!=(2k−2)∗(2k−4)∗(2k−6)....∗2 if n=2k−1 ⇒ (2k−1)∗(2k−3)∗(2k−5).....∗3∗1 for example 8!! =8∗6∗4∗2 =?? 9!! =9∗7∗5∗3∗1

$${n}!!\:\left({double}\:{factorial}\right) \\ $$$${if}\:{n}=\mathrm{2}{k}\:\Rightarrow \\ $$$$\left(\mathrm{2}{k}\right)!!=\left(\mathrm{2}{k}−\mathrm{2}\right)\ast\left(\mathrm{2}{k}−\mathrm{4}\right)\ast\left(\mathrm{2}{k}−\mathrm{6}\right)....\ast\mathrm{2} \\ $$$${if}\:{n}=\mathrm{2}{k}−\mathrm{1}\:\Rightarrow \\ $$$$\left(\mathrm{2}{k}−\mathrm{1}\right)\ast\left(\mathrm{2}{k}−\mathrm{3}\right)\ast\left(\mathrm{2}{k}−\mathrm{5}\right).....\ast\mathrm{3}\ast\mathrm{1} \\ $$$${for}\:\:{example} \\ $$$$\mathrm{8}!!\:=\mathrm{8}\ast\mathrm{6}\ast\mathrm{4}\ast\mathrm{2}\:=?? \\ $$$$\mathrm{9}!!\:=\mathrm{9}\ast\mathrm{7}\ast\mathrm{5}\ast\mathrm{3}\ast\mathrm{1} \\ $$

Commented by MJS_new last updated on 06/Sep/20

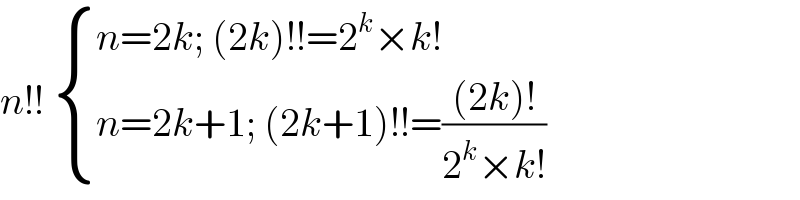
n!! { ((n=2k; (2k)!!=2^k ×k!)),((n=2k+1; (2k+1)!!=(((2k)!)/(2^k ×k!)))) :}

$${n}!!\:\begin{cases}{{n}=\mathrm{2}{k};\:\left(\mathrm{2}{k}\right)!!=\mathrm{2}^{{k}} ×{k}!}\\{{n}=\mathrm{2}{k}+\mathrm{1};\:\left(\mathrm{2}{k}+\mathrm{1}\right)!!=\frac{\left(\mathrm{2}{k}\right)!}{\mathrm{2}^{{k}} ×{k}!}}\end{cases} \\ $$

Answered by mnjuly1970 last updated on 06/Sep/20

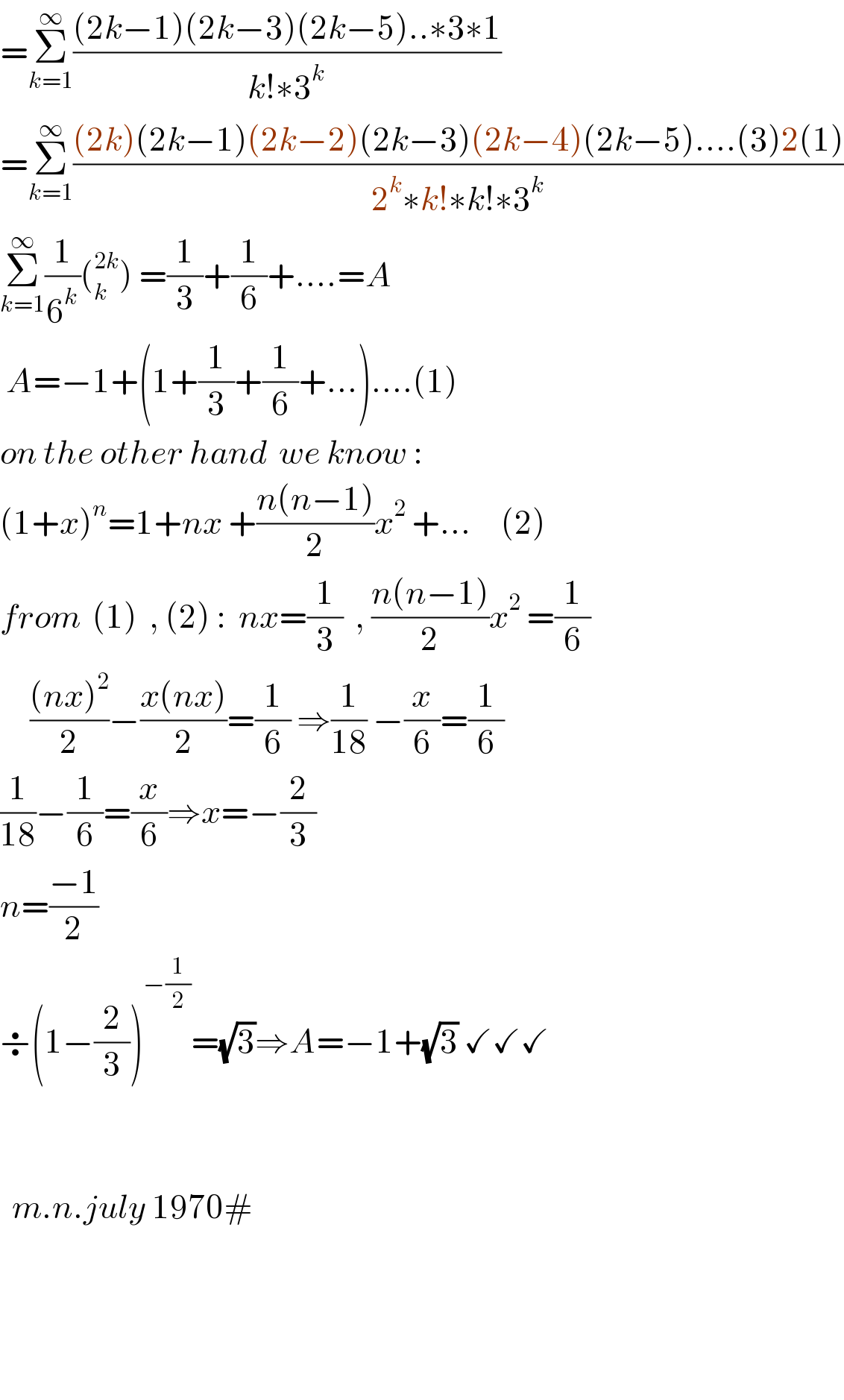
=Σ_(k=1) ^∞ (((2k−1)(2k−3)(2k−5)..∗3∗1)/(k!∗3^k )) =Σ_(k=1) ^∞ (((2k)(2k−1)(2k−2)(2k−3)(2k−4)(2k−5)....(3)2(1))/(2^k ∗k!∗k!∗3^k )) Σ_(k=1) ^∞ (1/6^k )(_k ^(2k) ) =(1/3)+(1/6)+....=A A=−1+(1+(1/3)+(1/6)+...)....(1) on the other hand we know : (1+x)^n =1+nx +((n(n−1))/2)x^2 +... (2) from (1) , (2) : nx=(1/3) , ((n(n−1))/2)x^2 =(1/6) (((nx)^2 )/2)−((x(nx))/2)=(1/6) ⇒(1/(18)) −(x/6)=(1/6) (1/(18))−(1/6)=(x/6)⇒x=−(2/3) n=((−1)/2) ÷(1−(2/3))^(−(1/2)) =(√3)⇒A=−1+(√3) ✓✓✓ m.n.july 1970#

$$=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(\mathrm{2}{k}−\mathrm{1}\right)\left(\mathrm{2}{k}−\mathrm{3}\right)\left(\mathrm{2}{k}−\mathrm{5}\right)..\ast\mathrm{3}\ast\mathrm{1}}{{k}!\ast\mathrm{3}^{{k}} } \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(\mathrm{2}{k}\right)\left(\mathrm{2}{k}−\mathrm{1}\right)\left(\mathrm{2}{k}−\mathrm{2}\right)\left(\mathrm{2}{k}−\mathrm{3}\right)\left(\mathrm{2}{k}−\mathrm{4}\right)\left(\mathrm{2}{k}−\mathrm{5}\right)....\left(\mathrm{3}\right)\mathrm{2}\left(\mathrm{1}\right)}{\mathrm{2}^{{k}} \ast{k}!\ast{k}!\ast\mathrm{3}^{{k}} } \\ $$$$\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{6}^{{k}} }\left(_{{k}} ^{\mathrm{2}{k}} \right)\:=\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{6}}+....={A} \\ $$$$\:{A}=−\mathrm{1}+\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{6}}+...\right)....\left(\mathrm{1}\right) \\ $$$${on}\:{the}\:{other}\:{hand}\:\:{we}\:{know}\:: \\ $$$$\left(\mathrm{1}+{x}\right)^{{n}} =\mathrm{1}+{nx}\:+\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}}{x}^{\mathrm{2}} \:+...\:\:\:\:\:\left(\mathrm{2}\right) \\ $$$${from}\:\:\left(\mathrm{1}\right)\:\:,\:\left(\mathrm{2}\right)\::\:\:{nx}=\frac{\mathrm{1}}{\mathrm{3}}\:\:,\:\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}}{x}^{\mathrm{2}} \:=\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\:\:\:\:\:\frac{\left({nx}\right)^{\mathrm{2}} }{\mathrm{2}}−\frac{{x}\left({nx}\right)}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{6}}\:\Rightarrow\frac{\mathrm{1}}{\mathrm{18}}\:−\frac{{x}}{\mathrm{6}}=\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\frac{\mathrm{1}}{\mathrm{18}}−\frac{\mathrm{1}}{\mathrm{6}}=\frac{{x}}{\mathrm{6}}\Rightarrow{x}=−\frac{\mathrm{2}}{\mathrm{3}} \\ $$$${n}=\frac{−\mathrm{1}}{\mathrm{2}} \\ $$$$\boldsymbol{\div}\left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} =\sqrt{\mathrm{3}}\Rightarrow{A}=−\mathrm{1}+\sqrt{\mathrm{3}}\:\checkmark\checkmark\checkmark \\ $$$$ \\ $$$$ \\ $$$$\:\:{m}.{n}.{july}\:\mathrm{1970}# \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by mohammad17 last updated on 07/Sep/20

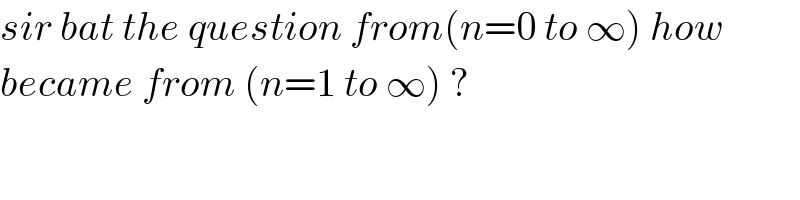
sir bat the question from(n=0 to ∞) how became from (n=1 to ∞) ?

$${sir}\:{bat}\:{the}\:{question}\:{from}\left({n}=\mathrm{0}\:{to}\:\infty\right)\:{how} \\ $$$${became}\:{from}\:\left({n}=\mathrm{1}\:{to}\:\infty\right)\:? \\ $$

Commented by mnjuly1970 last updated on 07/Sep/20

(−1)!! =!!!

$$\left(−\mathrm{1}\right)!!\:=!!! \\ $$$$ \\ $$

Commented by MJS_new last updated on 07/Sep/20

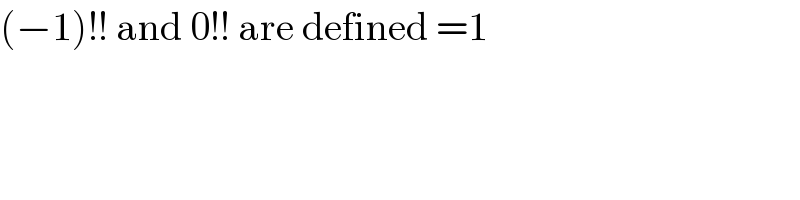
(−1)!! and 0!! are defined =1

$$\left(−\mathrm{1}\right)!!\:\mathrm{and}\:\mathrm{0}!!\:\mathrm{are}\:\mathrm{defined}\:=\mathrm{1} \\ $$

Commented by mohammad17 last updated on 07/Sep/20

thank you sir

$${thank}\:{you}\:{sir} \\ $$

Commented by mohammad17 last updated on 07/Sep/20

thank you sir

$${thank}\:{you}\:{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com