
Question Number 110939 by ajfour last updated on 31/Aug/20

Commented by ajfour last updated on 31/Aug/20
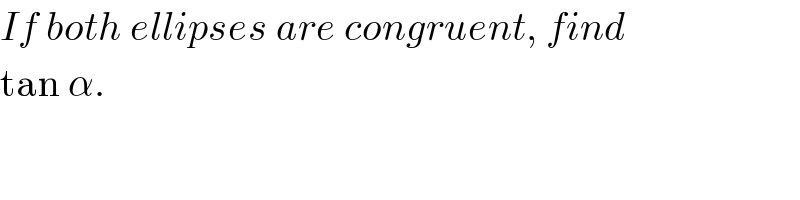
$${If}\:{both}\:{ellipses}\:{are}\:{congruent},\:{find} \\ $$$$\mathrm{tan}\:\alpha. \\ $$
Answered by ajfour last updated on 01/Sep/20

Answered by mr W last updated on 01/Sep/20
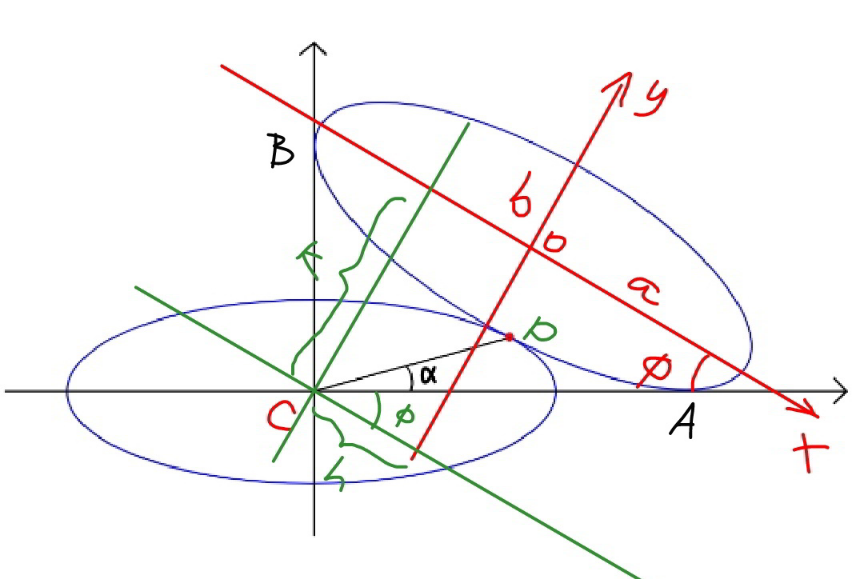
Commented by mr W last updated on 02/Sep/20
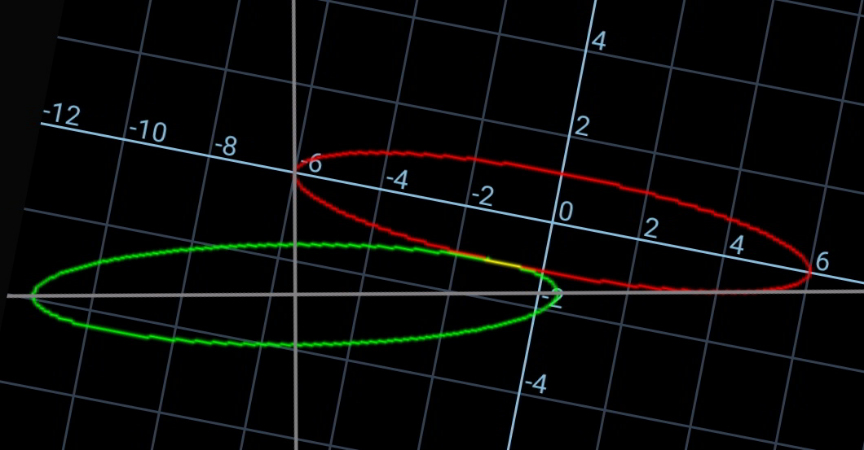
Commented by ajfour last updated on 02/Sep/20
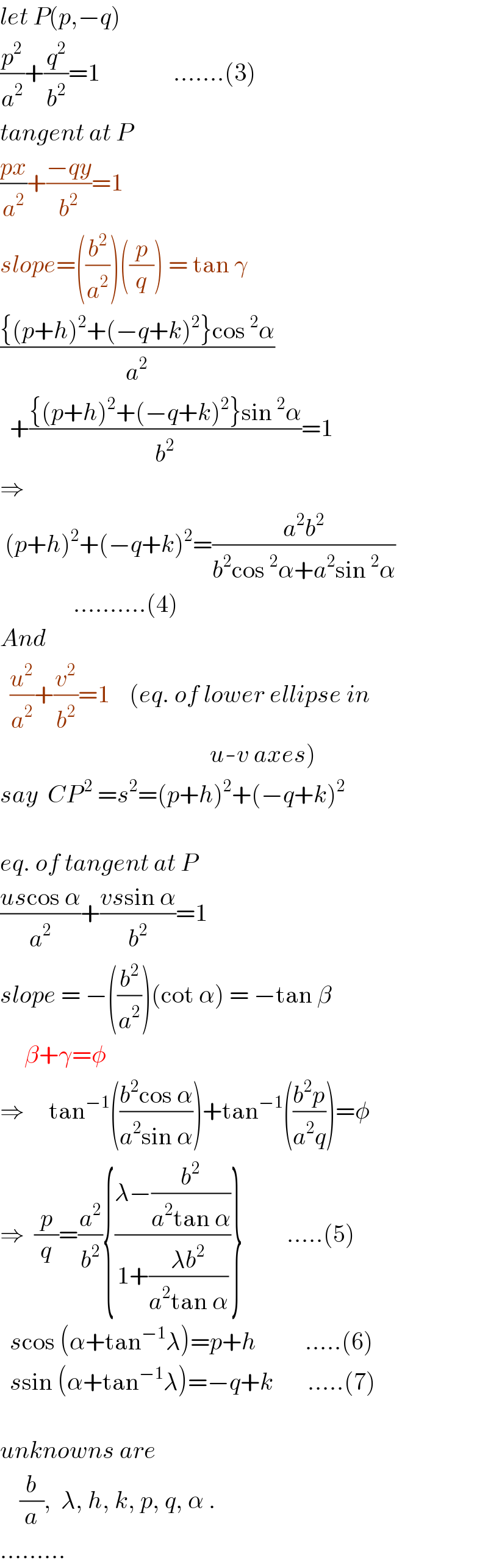
$${let}\:{P}\left({p},−{q}\right)\: \\ $$$$\frac{{p}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{q}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:.......\left(\mathrm{3}\right) \\ $$$${tangent}\:{at}\:{P} \\ $$$$\frac{{px}}{{a}^{\mathrm{2}} }+\frac{−{qy}}{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$${slope}=\left(\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right)\left(\frac{{p}}{{q}}\right)\:=\:\mathrm{tan}\:\gamma \\ $$$$\frac{\left\{\left({p}+{h}\right)^{\mathrm{2}} +\left(−{q}+{k}\right)^{\mathrm{2}} \right\}\mathrm{cos}\:^{\mathrm{2}} \alpha}{{a}^{\mathrm{2}} } \\ $$$$\:\:+\frac{\left\{\left({p}+{h}\right)^{\mathrm{2}} +\left(−{q}+{k}\right)^{\mathrm{2}} \right\}\mathrm{sin}\:^{\mathrm{2}} \alpha}{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\Rightarrow \\ $$$$\:\left({p}+{h}\right)^{\mathrm{2}} +\left(−{q}+{k}\right)^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{{b}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \alpha+{a}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \alpha} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:..........\left(\mathrm{4}\right) \\ $$$${And} \\ $$$$\:\:\frac{{u}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{v}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1}\:\:\:\:\left({eq}.\:{of}\:{lower}\:{ellipse}\:{in}\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{u}-{v}\:{axes}\right) \\ $$$${say}\:\:{CP}^{\:\mathrm{2}} \:={s}^{\mathrm{2}} =\left({p}+{h}\right)^{\mathrm{2}} +\left(−{q}+{k}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$${eq}.\:{of}\:{tangent}\:{at}\:{P} \\ $$$$\frac{{us}\mathrm{cos}\:\alpha}{{a}^{\mathrm{2}} }+\frac{{vs}\mathrm{sin}\:\alpha}{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$${slope}\:=\:−\left(\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right)\left(\mathrm{cot}\:\alpha\right)\:=\:−\mathrm{tan}\:\beta \\ $$$$\:\:\:\:\:\beta+\gamma=\phi \\ $$$$\Rightarrow\:\:\:\:\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{{b}^{\mathrm{2}} \mathrm{cos}\:\alpha}{{a}^{\mathrm{2}} \mathrm{sin}\:\alpha}\right)+\mathrm{tan}^{−\mathrm{1}} \left(\frac{{b}^{\mathrm{2}} {p}}{{a}^{\mathrm{2}} {q}}\right)=\phi \\ $$$$\Rightarrow\:\:\frac{{p}}{{q}}=\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\left\{\frac{\lambda−\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} \mathrm{tan}\:\alpha}}{\mathrm{1}+\frac{\lambda{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} \mathrm{tan}\:\alpha}}\right\}\:\:\:\:\:\:\:\:\:.....\left(\mathrm{5}\right) \\ $$$$\:\:{s}\mathrm{cos}\:\left(\alpha+\mathrm{tan}^{−\mathrm{1}} \lambda\right)={p}+{h}\:\:\:\:\:\:\:\:\:\:.....\left(\mathrm{6}\right) \\ $$$$\:\:{s}\mathrm{sin}\:\left(\alpha+\mathrm{tan}^{−\mathrm{1}} \lambda\right)=−{q}+{k}\:\:\:\:\:\:\:.....\left(\mathrm{7}\right) \\ $$$$ \\ $$$${unknowns}\:{are} \\ $$$$\:\:\:\:\frac{{b}}{{a}},\:\:\lambda,\:{h},\:{k},\:{p},\:{q},\:\alpha\:. \\ $$$$......... \\ $$
Commented by mr W last updated on 02/Sep/20
![eqn. of upper ellipse: (x^2 /a^2 )+(y^2 /b^2 )=1 ...(i) μ=(b/a) λ=tan φ C(−h,−k) eqn. of CA: y+k=(x+h)tan φ ⇒λx−y+λh−k=0 eqn. of CB: y+k=−((x+h)/(tan φ)) ⇒x+λy+h+λk=0 a^2 λ^2 +b^2 =(λh−k)^2 a^2 +b^2 λ^2 =(h+λk)^2 ⇒λh−k=+(√(a^2 λ^2 +b^2 )) ⇒h+λk=(√(a^2 +b^2 λ^2 )) ⇒h=((−λ(√(a^2 λ^2 +b^2 ))+(√(a^2 +b^2 λ^2 )))/(1+λ^2 )) ⇒η=(h/a)=((−λ(√(λ^2 +μ^2 ))+(√(1+μ^2 λ^2 )))/(1+λ^2 )) ⇒k=((λ(√(a^2 +b^2 λ^2 ))+(√(a^2 λ^2 +b^2 )))/( 1+λ^2 )) ⇒κ=(k/a)=((λ(√(1+μ^2 λ^2 ))+(√(λ^2 +μ^2 )))/( 1+λ^2 )) eqn. of lower ellipse: (([(x+h)cos φ+(y+k)sin φ]^2 )/a^2 )+(([−(x+h)sin φ+(y+k)cos φ]^2 )/b^2 )=1 (([(x+h)+(y+k)λ]^2 )/a^2 )+(([−(x+h)λ+(y+k)]^2 )/b^2 )=1+λ^2 ...(ii) (i) and (ii) should touch each other. let x=a cos θ, y=−b sin θ for point P ⇒[η+cos θ+(κ−μ sin θ)λ]^2 +(([κ−μ sin θ−(η+cos θ)λ]^2 )/μ^2 )=1+λ^2 ...(iii) for given μ we can determine λ such that (iii) has only one solution for θ. or for given λ we can determine μ.](Q111066.png)
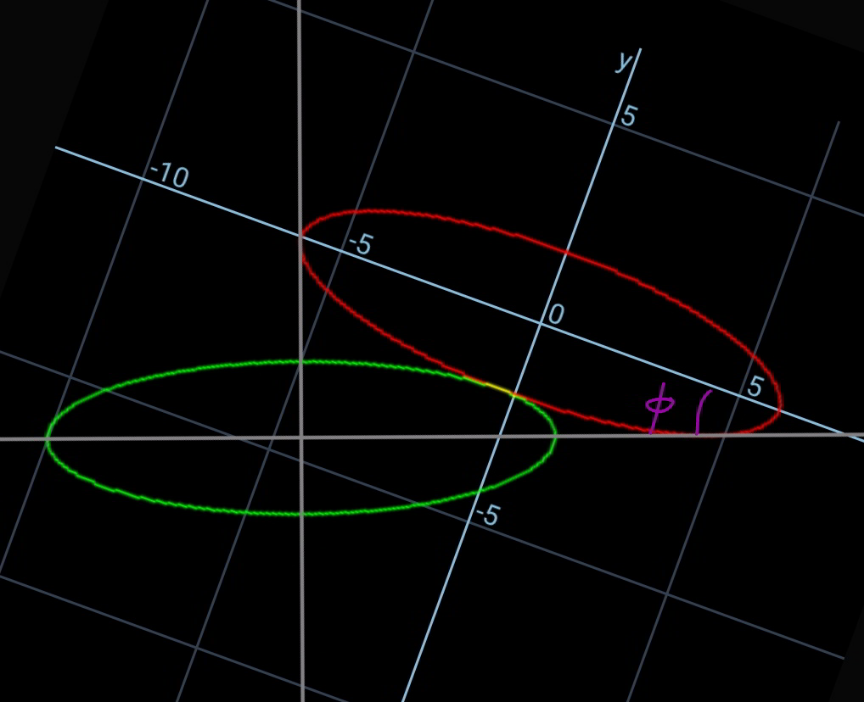
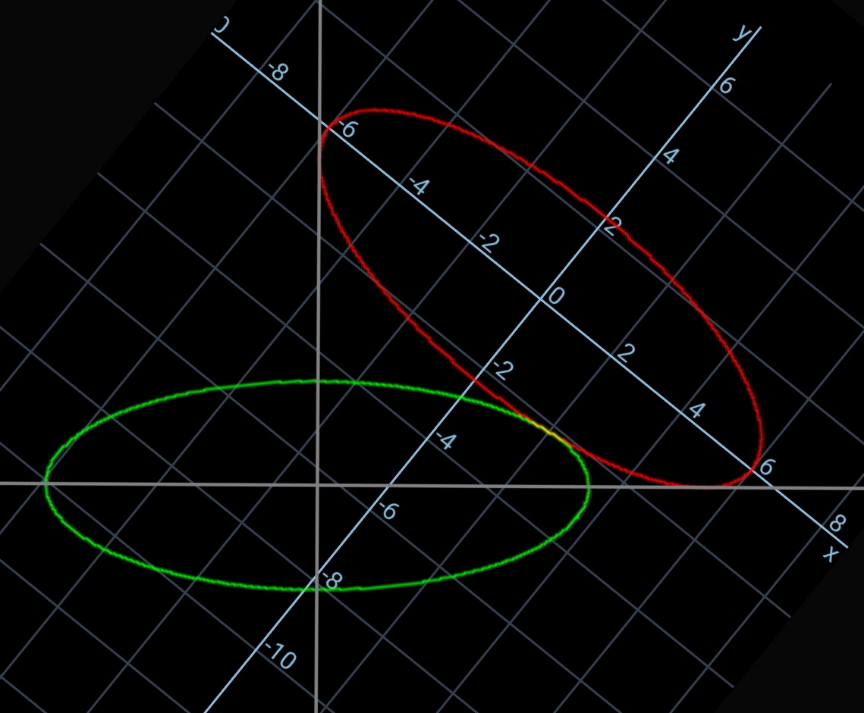
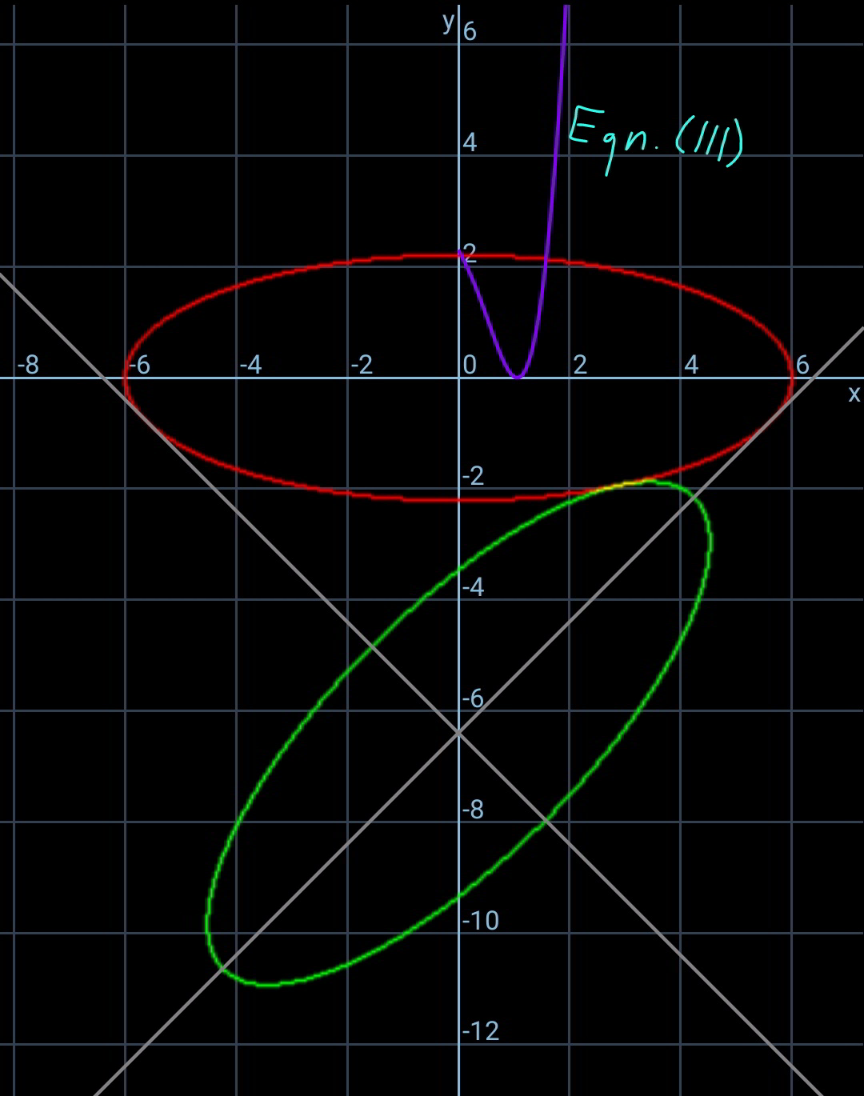
$${eqn}.\:{of}\:{upper}\:{ellipse}: \\ $$$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1}\:\:\:...\left({i}\right) \\ $$$$\mu=\frac{{b}}{{a}} \\ $$$$\lambda=\mathrm{tan}\:\phi \\ $$$${C}\left(−{h},−{k}\right) \\ $$$${eqn}.\:{of}\:{CA}: \\ $$$${y}+{k}=\left({x}+{h}\right)\mathrm{tan}\:\phi \\ $$$$\Rightarrow\lambda{x}−{y}+\lambda{h}−{k}=\mathrm{0} \\ $$$${eqn}.\:{of}\:{CB}: \\ $$$${y}+{k}=−\frac{{x}+{h}}{\mathrm{tan}\:\phi} \\ $$$$\Rightarrow{x}+\lambda{y}+{h}+\lambda{k}=\mathrm{0} \\ $$$$ \\ $$$${a}^{\mathrm{2}} \lambda^{\mathrm{2}} +{b}^{\mathrm{2}} =\left(\lambda{h}−{k}\right)^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} \lambda^{\mathrm{2}} =\left({h}+\lambda{k}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\lambda{h}−{k}=+\sqrt{{a}^{\mathrm{2}} \lambda^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$\Rightarrow{h}+\lambda{k}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} \lambda^{\mathrm{2}} } \\ $$$$\Rightarrow{h}=\frac{−\lambda\sqrt{{a}^{\mathrm{2}} \lambda^{\mathrm{2}} +{b}^{\mathrm{2}} }+\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} \lambda^{\mathrm{2}} }}{\mathrm{1}+\lambda^{\mathrm{2}} } \\ $$$$\Rightarrow\eta=\frac{{h}}{{a}}=\frac{−\lambda\sqrt{\lambda^{\mathrm{2}} +\mu^{\mathrm{2}} }+\sqrt{\mathrm{1}+\mu^{\mathrm{2}} \lambda^{\mathrm{2}} }}{\mathrm{1}+\lambda^{\mathrm{2}} } \\ $$$$\Rightarrow{k}=\frac{\lambda\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} \lambda^{\mathrm{2}} }+\sqrt{{a}^{\mathrm{2}} \lambda^{\mathrm{2}} +{b}^{\mathrm{2}} }}{\:\mathrm{1}+\lambda^{\mathrm{2}} } \\ $$$$\Rightarrow\kappa=\frac{{k}}{{a}}=\frac{\lambda\sqrt{\mathrm{1}+\mu^{\mathrm{2}} \lambda^{\mathrm{2}} }+\sqrt{\lambda^{\mathrm{2}} +\mu^{\mathrm{2}} }}{\:\mathrm{1}+\lambda^{\mathrm{2}} } \\ $$$$ \\ $$$${eqn}.\:{of}\:{lower}\:{ellipse}: \\ $$$$\frac{\left[\left({x}+{h}\right)\mathrm{cos}\:\phi+\left({y}+{k}\right)\mathrm{sin}\:\phi\right]^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{\left[−\left({x}+{h}\right)\mathrm{sin}\:\phi+\left({y}+{k}\right)\mathrm{cos}\:\phi\right]^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\frac{\left[\left({x}+{h}\right)+\left({y}+{k}\right)\lambda\right]^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{\left[−\left({x}+{h}\right)\lambda+\left({y}+{k}\right)\right]^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1}+\lambda^{\mathrm{2}} \:\:\:...\left({ii}\right) \\ $$$$\:\left({i}\right)\:{and}\:\left({ii}\right)\:{should}\:{touch}\:{each}\:{other}. \\ $$$$ \\ $$$${let}\:{x}={a}\:\mathrm{cos}\:\theta,\:{y}=−{b}\:\mathrm{sin}\:\theta\:{for}\:{point}\:{P} \\ $$$$\Rightarrow\left[\eta+\mathrm{cos}\:\theta+\left(\kappa−\mu\:\mathrm{sin}\:\theta\right)\lambda\right]^{\mathrm{2}} +\frac{\left[\kappa−\mu\:\mathrm{sin}\:\theta−\left(\eta+\mathrm{cos}\:\theta\right)\lambda\right]^{\mathrm{2}} }{\mu^{\mathrm{2}} }=\mathrm{1}+\lambda^{\mathrm{2}} \:\:\:...\left({iii}\right) \\ $$$${for}\:{given}\:\mu\:{we}\:{can}\:{determine}\:\lambda \\ $$$${such}\:{that}\:\left({iii}\right)\:{has}\:{only}\:{one}\:{solution} \\ $$$${for}\:\theta. \\ $$$${or}\:{for}\:{given}\:\lambda\:{we}\:{can}\:{determine}\:\mu. \\ $$
Commented by ajfour last updated on 02/Sep/20
$${Isn}'{t}\:{it}\:{okay}\:{Sir},\:\mathrm{7}\:{eqns}.\:\&\:\mathrm{7}\:{unknowns}.. \\ $$
Commented by mr W last updated on 02/Sep/20
$${it}'{s}\:{okay}\:{sir}!\:{let}\:{me}\:{see}\:{if}\:{we}\:{can}\: \\ $$$${simplify}\:{more}. \\ $$
Commented by mr W last updated on 02/Sep/20
Commented by mr W last updated on 02/Sep/20
Commented by mr W last updated on 02/Sep/20
Commented by ajfour last updated on 02/Sep/20
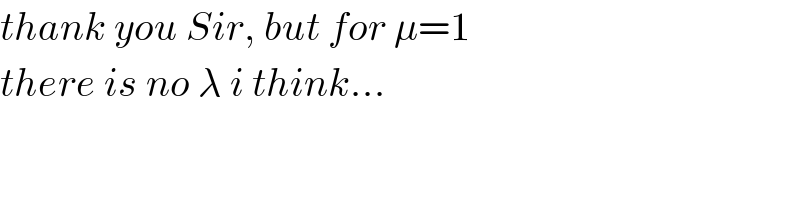
$${thank}\:{you}\:{Sir},\:{but}\:{for}\:\mu=\mathrm{1} \\ $$$${there}\:{is}\:{no}\:\lambda\:{i}\:{think}... \\ $$
Commented by mr W last updated on 02/Sep/20

$${correct}! \\ $$$$\mu_{{max}} \approx\mathrm{0}.\mathrm{38} \\ $$
