Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 110285 by mathdave last updated on 28/Aug/20

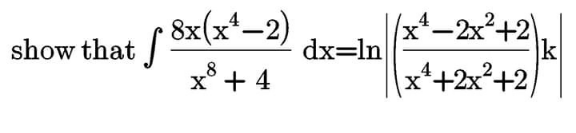
Answered by 1549442205PVT last updated on 29/Aug/20

we have x^8 +4=(x^4 +2)^2 −2x^4 = (x^4 +(√2) x^2 +2)(x^4 −(√2)x^2 +2) ((8x^5 −16x)/(x^8 +4))=((ax^3 +bx^2 +cx+d)/(x^4 −(√2)x^2 +2))+((a_1 x^3 +b_1 x^2 +c_1 x+d_1 )/(x^4 +(√2)x^2 +2)) =((ax^7 +bx^6 +(c+a(√2))x^5 +(b(√2)+d)x^4 +(2a+c(√2))x^3 +(2b+d(√2))x^2 +2cx+2d)/(x^8 +4)) +((a_1 x^7 +b_1 x^6 +(c_1 −a_1 (√2))x^5 (−b_1 (√2)+d_1 )x^4 +(2a_1 −c_1 (√2)x^3 +(2b_1 −d_1 (√2))x^2 +2c_1 x+2d_1 )/(x^8 +4)) ⇔ { (((a+a_1 )=0 (1))),(((b+b_1 ) =0 (2))),(((a−a_1 )(√2)+c+c_1 =8(3))),(((b−b_1 )(√2)+d+d_1 =0 (4))),((2(a+a_1 )+(c−c_1 )(√2)=0(5))),(((d−d_1 )(√2)+2(b+b_1 )=0(6))),((2(c+c_1 )=−16(7))),((d+d_1 =0 (8))) :} (5)(1)⇒c=c_1 ;(1)(3)(7)⇔a=4(√2) ,a_1 =−4(√2) (1)(5)(6)⇒c=c_1 =−4,(2)(6)(8)⇒d=d_1 =0 Therefore ((8x^5 −16x)/(x^8 +4))=((4(√2) x^3 −4)/(x^4 −(√2)x^2 +2))+((−4(√2)x^3 −4)/(x^4 +(√2)x^2 +2)) ∫((8x^5 −16x)/(x^8 +4))dx=(√2)∫((4x^3 −2(√2))/(x^4 −(√2)x^2 +2))dx−(√2)∫((4 x^3 +2(√2))/(x^4 +(√2)x^2 +2))dx+ =(√2)∫ ((dx^4 −(√2)x^2 +2))/(x^4 −(√2)x^2 +2))−(√2)∫ ((d(x^4 −(√2)x^2 +2))/(x^4 −(√2)x^2 +2))dx =(√2)ln∣x^4 −(√2)x^2 +2∣−(√2)ln∣x^4 +(√2)x^2 +2∣ =(√2)ln∣((x^4 −(√2)x^2 +2)/(x^4 −(√2)x^2 +2))∣

$$\mathrm{we}\:\mathrm{have}\:\mathrm{x}^{\mathrm{8}} +\mathrm{4}=\left(\mathrm{x}^{\mathrm{4}} +\mathrm{2}\right)^{\mathrm{2}} −\mathrm{2x}^{\mathrm{4}} = \\ $$$$\left(\mathrm{x}^{\mathrm{4}} +\sqrt{\mathrm{2}}\:\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)\left(\mathrm{x}^{\mathrm{4}} −\sqrt{\mathrm{2}}\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right) \\ $$$$\frac{\mathrm{8x}^{\mathrm{5}} −\mathrm{16x}}{\mathrm{x}^{\mathrm{8}} +\mathrm{4}}=\frac{\mathrm{ax}^{\mathrm{3}} +\mathrm{bx}^{\mathrm{2}} +\mathrm{cx}+\mathrm{d}}{\mathrm{x}^{\mathrm{4}} −\sqrt{\mathrm{2}}\mathrm{x}^{\mathrm{2}} +\mathrm{2}}+\frac{\mathrm{a}_{\mathrm{1}} \mathrm{x}^{\mathrm{3}} +\mathrm{b}_{\mathrm{1}} \mathrm{x}^{\mathrm{2}} +\mathrm{c}_{\mathrm{1}} \mathrm{x}+\mathrm{d}_{\mathrm{1}} }{\mathrm{x}^{\mathrm{4}} +\sqrt{\mathrm{2}}\mathrm{x}^{\mathrm{2}} +\mathrm{2}} \\ $$$$=\frac{\mathrm{ax}^{\mathrm{7}} +\mathrm{bx}^{\mathrm{6}} +\left(\mathrm{c}+\mathrm{a}\sqrt{\mathrm{2}}\right)\mathrm{x}^{\mathrm{5}} +\left(\mathrm{b}\sqrt{\mathrm{2}}+\mathrm{d}\right)\mathrm{x}^{\mathrm{4}} +\left(\mathrm{2a}+\mathrm{c}\sqrt{\mathrm{2}}\right)\mathrm{x}^{\mathrm{3}} +\left(\mathrm{2b}+\mathrm{d}\sqrt{\mathrm{2}}\right)\mathrm{x}^{\mathrm{2}} +\mathrm{2cx}+\mathrm{2d}}{\mathrm{x}^{\mathrm{8}} +\mathrm{4}} \\ $$$$+\frac{\mathrm{a}_{\mathrm{1}} \mathrm{x}^{\mathrm{7}} +\mathrm{b}_{\mathrm{1}} \mathrm{x}^{\mathrm{6}} +\left(\mathrm{c}_{\mathrm{1}} −\mathrm{a}_{\mathrm{1}} \sqrt{\mathrm{2}}\right)\mathrm{x}^{\mathrm{5}} \left(−\mathrm{b}_{\mathrm{1}} \sqrt{\mathrm{2}}+\mathrm{d}_{\mathrm{1}} \right)\mathrm{x}^{\mathrm{4}} +\left(\mathrm{2a}_{\mathrm{1}} −\mathrm{c}_{\mathrm{1}} \sqrt{\mathrm{2}}\mathrm{x}^{\mathrm{3}} +\left(\mathrm{2b}_{\mathrm{1}} −\mathrm{d}_{\mathrm{1}} \sqrt{\mathrm{2}}\right)\mathrm{x}^{\mathrm{2}} +\mathrm{2c}_{\mathrm{1}} \mathrm{x}+\mathrm{2d}_{\mathrm{1}} \right.}{\mathrm{x}^{\mathrm{8}} +\mathrm{4}} \\ $$$$\Leftrightarrow\begin{cases}{\left(\mathrm{a}+\mathrm{a}_{\mathrm{1}} \right)=\mathrm{0}\:\left(\mathrm{1}\right)}\\{\left(\mathrm{b}+\mathrm{b}_{\mathrm{1}} \right)\:=\mathrm{0}\:\left(\mathrm{2}\right)}\\{\left(\mathrm{a}−\mathrm{a}_{\mathrm{1}} \right)\sqrt{\mathrm{2}}+\mathrm{c}+\mathrm{c}_{\mathrm{1}} =\mathrm{8}\left(\mathrm{3}\right)}\\{\left(\mathrm{b}−\mathrm{b}_{\mathrm{1}} \right)\sqrt{\mathrm{2}}+\mathrm{d}+\mathrm{d}_{\mathrm{1}} =\mathrm{0}\:\left(\mathrm{4}\right)}\\{\mathrm{2}\left(\mathrm{a}+\mathrm{a}_{\mathrm{1}} \right)+\left(\mathrm{c}−\mathrm{c}_{\mathrm{1}} \right)\sqrt{\mathrm{2}}=\mathrm{0}\left(\mathrm{5}\right)}\\{\left(\mathrm{d}−\mathrm{d}_{\mathrm{1}} \right)\sqrt{\mathrm{2}}+\mathrm{2}\left(\mathrm{b}+\mathrm{b}_{\mathrm{1}} \right)=\mathrm{0}\left(\mathrm{6}\right)}\\{\mathrm{2}\left(\mathrm{c}+\mathrm{c}_{\mathrm{1}} \right)=−\mathrm{16}\left(\mathrm{7}\right)}\\{\mathrm{d}+\mathrm{d}_{\mathrm{1}} =\mathrm{0}\:\left(\mathrm{8}\right)}\end{cases} \\ $$$$\left(\mathrm{5}\right)\left(\mathrm{1}\right)\Rightarrow\mathrm{c}=\mathrm{c}_{\mathrm{1}} ;\left(\mathrm{1}\right)\left(\mathrm{3}\right)\left(\mathrm{7}\right)\Leftrightarrow\mathrm{a}=\mathrm{4}\sqrt{\mathrm{2}}\:,\mathrm{a}_{\mathrm{1}} =−\mathrm{4}\sqrt{\mathrm{2}}\: \\ $$$$\left(\mathrm{1}\right)\left(\mathrm{5}\right)\left(\mathrm{6}\right)\Rightarrow\mathrm{c}=\mathrm{c}_{\mathrm{1}} =−\mathrm{4},\left(\mathrm{2}\right)\left(\mathrm{6}\right)\left(\mathrm{8}\right)\Rightarrow\mathrm{d}=\mathrm{d}_{\mathrm{1}} =\mathrm{0} \\ $$$$\mathrm{Therefore} \\ $$$$\frac{\mathrm{8x}^{\mathrm{5}} −\mathrm{16x}}{\mathrm{x}^{\mathrm{8}} +\mathrm{4}}=\frac{\mathrm{4}\sqrt{\mathrm{2}}\:\mathrm{x}^{\mathrm{3}} −\mathrm{4}}{\mathrm{x}^{\mathrm{4}} −\sqrt{\mathrm{2}}\mathrm{x}^{\mathrm{2}} +\mathrm{2}}+\frac{−\mathrm{4}\sqrt{\mathrm{2}}\mathrm{x}^{\mathrm{3}} −\mathrm{4}}{\mathrm{x}^{\mathrm{4}} +\sqrt{\mathrm{2}}\mathrm{x}^{\mathrm{2}} +\mathrm{2}} \\ $$$$\int\frac{\mathrm{8x}^{\mathrm{5}} −\mathrm{16x}}{\mathrm{x}^{\mathrm{8}} +\mathrm{4}}\mathrm{dx}=\sqrt{\mathrm{2}}\int\frac{\mathrm{4x}^{\mathrm{3}} −\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{x}^{\mathrm{4}} −\sqrt{\mathrm{2}}\mathrm{x}^{\mathrm{2}} +\mathrm{2}}\mathrm{dx}−\sqrt{\mathrm{2}}\int\frac{\mathrm{4}\:\mathrm{x}^{\mathrm{3}} +\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{x}^{\mathrm{4}} +\sqrt{\mathrm{2}}\mathrm{x}^{\mathrm{2}} +\mathrm{2}}\mathrm{dx}+ \\ $$$$=\sqrt{\mathrm{2}}\int\:\frac{\left.\mathrm{dx}^{\mathrm{4}} −\sqrt{\mathrm{2}}\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)}{\mathrm{x}^{\mathrm{4}} −\sqrt{\mathrm{2}}\mathrm{x}^{\mathrm{2}} +\mathrm{2}}−\sqrt{\mathrm{2}}\int\:\frac{\mathrm{d}\left(\mathrm{x}^{\mathrm{4}} −\sqrt{\mathrm{2}}\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)}{\mathrm{x}^{\mathrm{4}} −\sqrt{\mathrm{2}}\mathrm{x}^{\mathrm{2}} +\mathrm{2}}\mathrm{dx} \\ $$$$=\sqrt{\mathrm{2}}\mathrm{ln}\mid\mathrm{x}^{\mathrm{4}} −\sqrt{\mathrm{2}}\mathrm{x}^{\mathrm{2}} +\mathrm{2}\mid−\sqrt{\mathrm{2}}\mathrm{ln}\mid\mathrm{x}^{\mathrm{4}} +\sqrt{\mathrm{2}}\mathrm{x}^{\mathrm{2}} +\mathrm{2}\mid \\ $$$$=\sqrt{\mathrm{2}}\boldsymbol{\mathrm{ln}}\mid\frac{\boldsymbol{\mathrm{x}}^{\mathrm{4}} −\sqrt{\mathrm{2}}\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{2}}{\boldsymbol{\mathrm{x}}^{\mathrm{4}} −\sqrt{\mathrm{2}}\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{2}}\mid \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com