Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 109922 by Ar Brandon last updated on 26/Aug/20

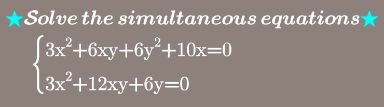
Answered by 1549442205PVT last updated on 26/Aug/20

3x^2 +12xy+6y=0⇔x^2 +4xy+2y=0(1) i)Case x=0⇒y=0 substituting into first eqn. we see it satisfy,so we get y=0⇒(x,y)=(0,0)is a root ii)Case x≠0.From (1)we get y=((−x^2 )/(4x+2))(2) .Replace into first eqn. 3x^2 +6x.((−x^2 )/(4x+2))+6.(x^4 /(16x^2 +16x+4))+10x=0 ⇔6x^4 +48x^4 +48x^3 +12x^2 +160x^3 +160x^2 +40x−24x^4 −12x^3 =0 ⇔30x^4 +196x^3 +172x^2 +40x=0 ⇔15x^3 +98x^2 +86x+20=0.Multiplying two sides by 15^2 and put 15x=t we get t^3 +98t^2 +1290t+4500=0.Set t=u−((98)/3) After some simple transformation we obtain u^3 −((5734)/3)u+((866104)/(27))=0(∗) Putting u=(2/3)(√(5734))×z replace into (∗)we get ((8.5734(√(5734)))/(27))z^3 −((2.5734.(√(5734)))/9)z+((866104)/(27))=0 Multiplying two sides by ((27)/(2.5734(√(5734)))) we get 4z^3 −3z+((216526)/(2867(√(5734))))=0(∗∗).On the other hands,we have 4cos^3 v−3cosv−cos3v=0 .Hence Putting cos3v=((−216526)/(2867(√(5734)))) (3) we infer cosv are roots of (∗∗) (3)⇔3v=cos^(−1) (((−216526)/(2867(√(5734)))))+2kπ ⇔v=(1/3)[cos^(−1) (((−216526)/(2867(√(5734)))))+2kπ](k=0,1,2) Thus z=cosv=cos{(1/3)[cos^(−1) (((−216526)/(2867(√(5734)))))+2kπ]} are three different roots of (∗∗).Hence u=(2/3)(√(5734)) z=(2/3)(√(5734))cos{(1/3)[cos^(−1) (((−216526)/(2867(√(5734)))))+2kπ]}(k=0..2^(−) ) are three roots of (∗).From that we get x=((u−98/3)/(15))=(((2/3)(√(5734 )) cos{(1/3)[cos^(−1) (((−216526)/(2867(√(5734)))))+2kπ]}−((98)/3))/(15)) are three different roots of equation 15x^3 +98x^2 +86x+20=0 Replace into (2) we get corresponding values of y and obtain roots of given system

$$\mathrm{3x}^{\mathrm{2}} +\mathrm{12xy}+\mathrm{6y}=\mathrm{0}\Leftrightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{4xy}+\mathrm{2y}=\mathrm{0}\left(\mathrm{1}\right) \\ $$$$\left.\mathrm{i}\right)\mathrm{Case}\:\mathrm{x}=\mathrm{0}\Rightarrow\mathrm{y}=\mathrm{0}\:\mathrm{substituting}\:\mathrm{into}\:\mathrm{first}\:\mathrm{eqn}. \\ $$$$\mathrm{we}\:\mathrm{see}\:\mathrm{it}\:\mathrm{satisfy},\mathrm{so} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{y}=\mathrm{0}\Rightarrow\left(\mathrm{x},\mathrm{y}\right)=\left(\mathrm{0},\mathrm{0}\right)\mathrm{is}\:\mathrm{a}\:\mathrm{root} \\ $$$$\left.\mathrm{ii}\right)\mathrm{Case}\:\mathrm{x}\neq\mathrm{0}.\mathrm{From}\:\left(\mathrm{1}\right)\mathrm{we}\:\mathrm{get}\:\mathrm{y}=\frac{−\mathrm{x}^{\mathrm{2}} }{\mathrm{4x}+\mathrm{2}}\left(\mathrm{2}\right) \\ $$$$.\mathrm{Replace}\:\mathrm{into}\:\mathrm{first}\:\mathrm{eqn}. \\ $$$$\mathrm{3x}^{\mathrm{2}} +\mathrm{6x}.\frac{−\mathrm{x}^{\mathrm{2}} }{\mathrm{4x}+\mathrm{2}}+\mathrm{6}.\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{16x}^{\mathrm{2}} +\mathrm{16x}+\mathrm{4}}+\mathrm{10x}=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{6x}^{\mathrm{4}} +\mathrm{48x}^{\mathrm{4}} +\mathrm{48x}^{\mathrm{3}} +\mathrm{12x}^{\mathrm{2}} +\mathrm{160x}^{\mathrm{3}} +\mathrm{160x}^{\mathrm{2}} +\mathrm{40x}−\mathrm{24x}^{\mathrm{4}} −\mathrm{12x}^{\mathrm{3}} =\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{30x}^{\mathrm{4}} +\mathrm{196x}^{\mathrm{3}} +\mathrm{172x}^{\mathrm{2}} +\mathrm{40x}=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{15x}^{\mathrm{3}} +\mathrm{98x}^{\mathrm{2}} +\mathrm{86x}+\mathrm{20}=\mathrm{0}.\mathrm{Multiplying} \\ $$$$\mathrm{two}\:\mathrm{sides}\:\mathrm{by}\:\mathrm{15}^{\mathrm{2}} \mathrm{and}\:\mathrm{put}\:\mathrm{15x}=\mathrm{t}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{t}^{\mathrm{3}} +\mathrm{98t}^{\mathrm{2}} +\mathrm{1290t}+\mathrm{4500}=\mathrm{0}.\mathrm{Set}\:\mathrm{t}=\mathrm{u}−\frac{\mathrm{98}}{\mathrm{3}} \\ $$$$\mathrm{After}\:\mathrm{some}\:\mathrm{simple}\:\mathrm{transformation}\:\mathrm{we} \\ $$$$\mathrm{obtain}\:\mathrm{u}^{\mathrm{3}} −\frac{\mathrm{5734}}{\mathrm{3}}\mathrm{u}+\frac{\mathrm{866104}}{\mathrm{27}}=\mathrm{0}\left(\ast\right) \\ $$$$\mathrm{Putting}\:\mathrm{u}=\frac{\mathrm{2}}{\mathrm{3}}\sqrt{\mathrm{5734}}×\mathrm{z}\:\mathrm{replace}\:\mathrm{into} \\ $$$$\left(\ast\right)\mathrm{we}\:\mathrm{get}\:\frac{\mathrm{8}.\mathrm{5734}\sqrt{\mathrm{5734}}}{\mathrm{27}}\mathrm{z}^{\mathrm{3}} −\frac{\mathrm{2}.\mathrm{5734}.\sqrt{\mathrm{5734}}}{\mathrm{9}}\mathrm{z}+\frac{\mathrm{866104}}{\mathrm{27}}=\mathrm{0} \\ $$$$\mathrm{Multiplying}\:\mathrm{two}\:\mathrm{sides}\:\mathrm{by}\:\frac{\mathrm{27}}{\mathrm{2}.\mathrm{5734}\sqrt{\mathrm{5734}}} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{4z}^{\mathrm{3}} −\mathrm{3z}+\frac{\mathrm{216526}}{\mathrm{2867}\sqrt{\mathrm{5734}}}=\mathrm{0}\left(\ast\ast\right).\mathrm{On}\:\mathrm{the} \\ $$$$\mathrm{other}\:\mathrm{hands},\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{4cos}^{\mathrm{3}} \mathrm{v}−\mathrm{3cosv}−\mathrm{cos3v}=\mathrm{0}\:.\mathrm{Hence} \\ $$$$\mathrm{Putting}\:\mathrm{cos3v}=\frac{−\mathrm{216526}}{\mathrm{2867}\sqrt{\mathrm{5734}}}\:\left(\mathrm{3}\right)\:\mathrm{we}\:\mathrm{infer} \\ $$$$\mathrm{cosv}\:\mathrm{are}\:\mathrm{roots}\:\mathrm{of}\:\left(\ast\ast\right) \\ $$$$\left(\mathrm{3}\right)\Leftrightarrow\mathrm{3v}=\mathrm{cos}^{−\mathrm{1}} \left(\frac{−\mathrm{216526}}{\mathrm{2867}\sqrt{\mathrm{5734}}}\right)+\mathrm{2k}\pi \\ $$$$\Leftrightarrow\mathrm{v}=\frac{\mathrm{1}}{\mathrm{3}}\left[\mathrm{cos}^{−\mathrm{1}} \left(\frac{−\mathrm{216526}}{\mathrm{2867}\sqrt{\mathrm{5734}}}\right)+\mathrm{2k}\pi\right]\left(\mathrm{k}=\mathrm{0},\mathrm{1},\mathrm{2}\right) \\ $$$$\mathrm{Thus}\:\mathrm{z}=\mathrm{cosv}=\mathrm{cos}\left\{\frac{\mathrm{1}}{\mathrm{3}}\left[\mathrm{cos}^{−\mathrm{1}} \left(\frac{−\mathrm{216526}}{\mathrm{2867}\sqrt{\mathrm{5734}}}\right)+\mathrm{2k}\pi\right]\right\} \\ $$$$\mathrm{are}\:\mathrm{three}\:\mathrm{different}\:\mathrm{roots}\:\mathrm{of}\:\left(\ast\ast\right).\mathrm{Hence} \\ $$$$\mathrm{u}=\frac{\mathrm{2}}{\mathrm{3}}\sqrt{\mathrm{5734}}\:\mathrm{z}=\frac{\mathrm{2}}{\mathrm{3}}\sqrt{\mathrm{5734}}\mathrm{cos}\left\{\frac{\mathrm{1}}{\mathrm{3}}\left[\mathrm{cos}^{−\mathrm{1}} \left(\frac{−\mathrm{216526}}{\mathrm{2867}\sqrt{\mathrm{5734}}}\right)+\mathrm{2k}\pi\right]\right\}\left(\mathrm{k}=\overline {\mathrm{0}..\mathrm{2}}\right) \\ $$$$\mathrm{are}\:\mathrm{three}\:\mathrm{roots}\:\mathrm{of}\:\left(\ast\right).\mathrm{From}\:\mathrm{that}\:\mathrm{we} \\ $$$$\mathrm{get}\:\mathrm{x}=\frac{\mathrm{u}−\mathrm{98}/\mathrm{3}}{\mathrm{15}}=\frac{\frac{\mathrm{2}}{\mathrm{3}}\sqrt{\mathrm{5734}\:}\:\mathrm{cos}\left\{\frac{\mathrm{1}}{\mathrm{3}}\left[\mathrm{cos}^{−\mathrm{1}} \left(\frac{−\mathrm{216526}}{\mathrm{2867}\sqrt{\mathrm{5734}}}\right)+\mathrm{2k}\pi\right]\right\}−\frac{\mathrm{98}}{\mathrm{3}}}{\mathrm{15}} \\ $$$$\boldsymbol{\mathrm{are}}\:\boldsymbol{\mathrm{three}}\:\boldsymbol{\mathrm{different}}\:\boldsymbol{\mathrm{roots}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{equation}} \\ $$$$\mathrm{15}\boldsymbol{\mathrm{x}}^{\mathrm{3}} +\mathrm{98}\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{86}\boldsymbol{\mathrm{x}}+\mathrm{20}=\mathrm{0}\: \\ $$$$\boldsymbol{\mathrm{Replace}}\:\boldsymbol{\mathrm{into}}\:\left(\mathrm{2}\right)\:\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{get}}\:\boldsymbol{\mathrm{corresponding}}\:\boldsymbol{\mathrm{values}} \\ $$$$\mathrm{of}\:\mathrm{y}\:\mathrm{and}\:\mathrm{obtain}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{given}\:\mathrm{system} \\ $$

Commented by Ar Brandon last updated on 27/Aug/20

Thanks so much, Sir.

Terms of Service

Privacy Policy

Contact: info@tinkutara.com