
Question Number 109400 by mohammad17 last updated on 23/Aug/20
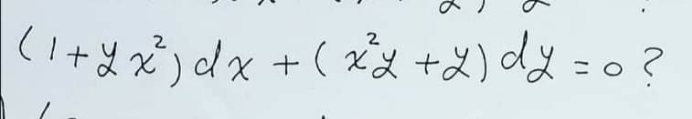
Commented by mohammad17 last updated on 23/Aug/20

$${help}\:{me}\:{sir}? \\ $$
Commented by bobhans last updated on 23/Aug/20
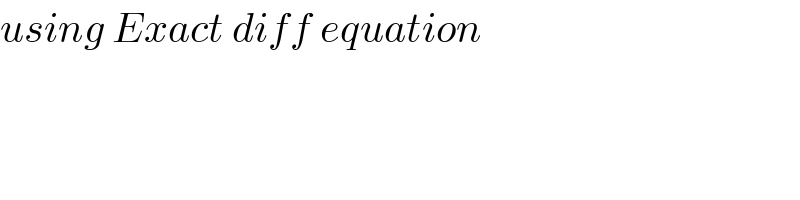
$${using}\:{Exact}\:{diff}\:{equation} \\ $$
Commented by mohammad17 last updated on 23/Aug/20
$${sir}\:{the}\:{equation}\:{is}\:{not}\:{exact}\:? \\ $$$${are}\:{you}\:{can}\:{help}\:{me}\:? \\ $$
Commented by mohammad17 last updated on 23/Aug/20
$${no}\:{one}\:{here}\:{can}\:{you}\:{solve}\:{this}\:? \\ $$
Answered by ajfour last updated on 24/Aug/20
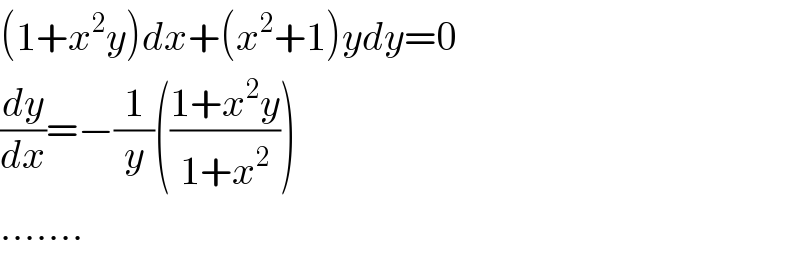
$$\left(\mathrm{1}+{x}^{\mathrm{2}} {y}\right){dx}+\left({x}^{\mathrm{2}} +\mathrm{1}\right){ydy}=\mathrm{0} \\ $$$$\frac{{dy}}{{dx}}=−\frac{\mathrm{1}}{{y}}\left(\frac{\mathrm{1}+{x}^{\mathrm{2}} {y}}{\mathrm{1}+{x}^{\mathrm{2}} }\right) \\ $$$$....... \\ $$
