Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 107999 by Don08q last updated on 13/Aug/20

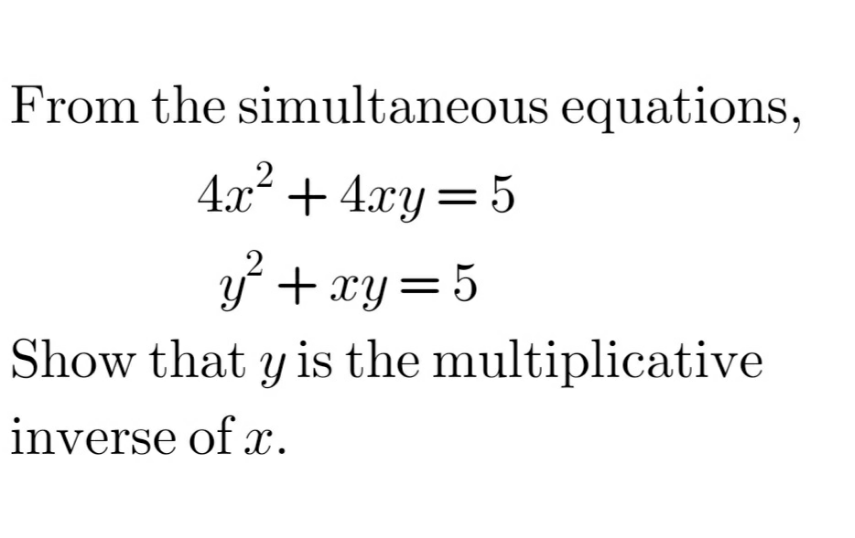
Commented by udaythool last updated on 13/Aug/20

⇒4x^2 +3xy−y^2 =0 ⇒(x+y)(4x−y)=0 ⇒4x=y; (∵ x+y≠0) ⇒4x^2 =xy ⇒5xy=5 ⇒xy=1

$$\Rightarrow\mathrm{4}{x}^{\mathrm{2}} +\mathrm{3}{xy}−{y}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\left({x}+{y}\right)\left(\mathrm{4}{x}−{y}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{4}{x}={y};\:\:\:\left(\because\:{x}+{y}\neq\mathrm{0}\right) \\ $$$$\Rightarrow\mathrm{4}{x}^{\mathrm{2}} ={xy} \\ $$$$\Rightarrow\mathrm{5}{xy}=\mathrm{5} \\ $$$$\Rightarrow{xy}=\mathrm{1} \\ $$

Commented by Don08q last updated on 13/Aug/20

Thanks Sir

$${Thanks}\:{Sir} \\ $$

Commented by Rasheed.Sindhi last updated on 13/Aug/20

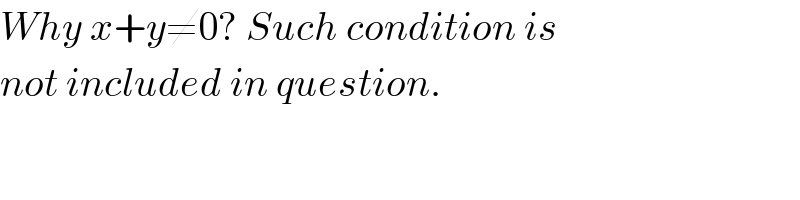
Why x+y≠0? Such condition is not included in question.

$${Why}\:{x}+{y}\neq\mathrm{0}?\:{Such}\:{condition}\:{is} \\ $$$${not}\:{included}\:{in}\:{question}. \\ $$

Commented by Sarah85 last updated on 13/Aug/20

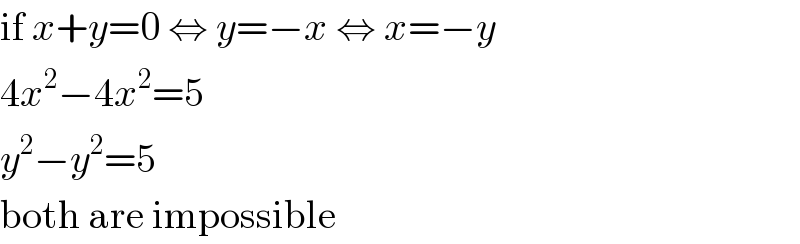
if x+y=0 ⇔ y=−x ⇔ x=−y 4x^2 −4x^2 =5 y^2 −y^2 =5 both are impossible

$$\mathrm{if}\:{x}+{y}=\mathrm{0}\:\Leftrightarrow\:{y}=−{x}\:\Leftrightarrow\:{x}=−{y} \\ $$$$\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}{x}^{\mathrm{2}} =\mathrm{5} \\ $$$${y}^{\mathrm{2}} −{y}^{\mathrm{2}} =\mathrm{5} \\ $$$$\mathrm{both}\:\mathrm{are}\:\mathrm{impossible} \\ $$

Commented by Rasheed.Sindhi last updated on 14/Aug/20

THANKS madam!

$$\mathcal{THANKS}\:{madam}! \\ $$

Answered by Sarah85 last updated on 13/Aug/20

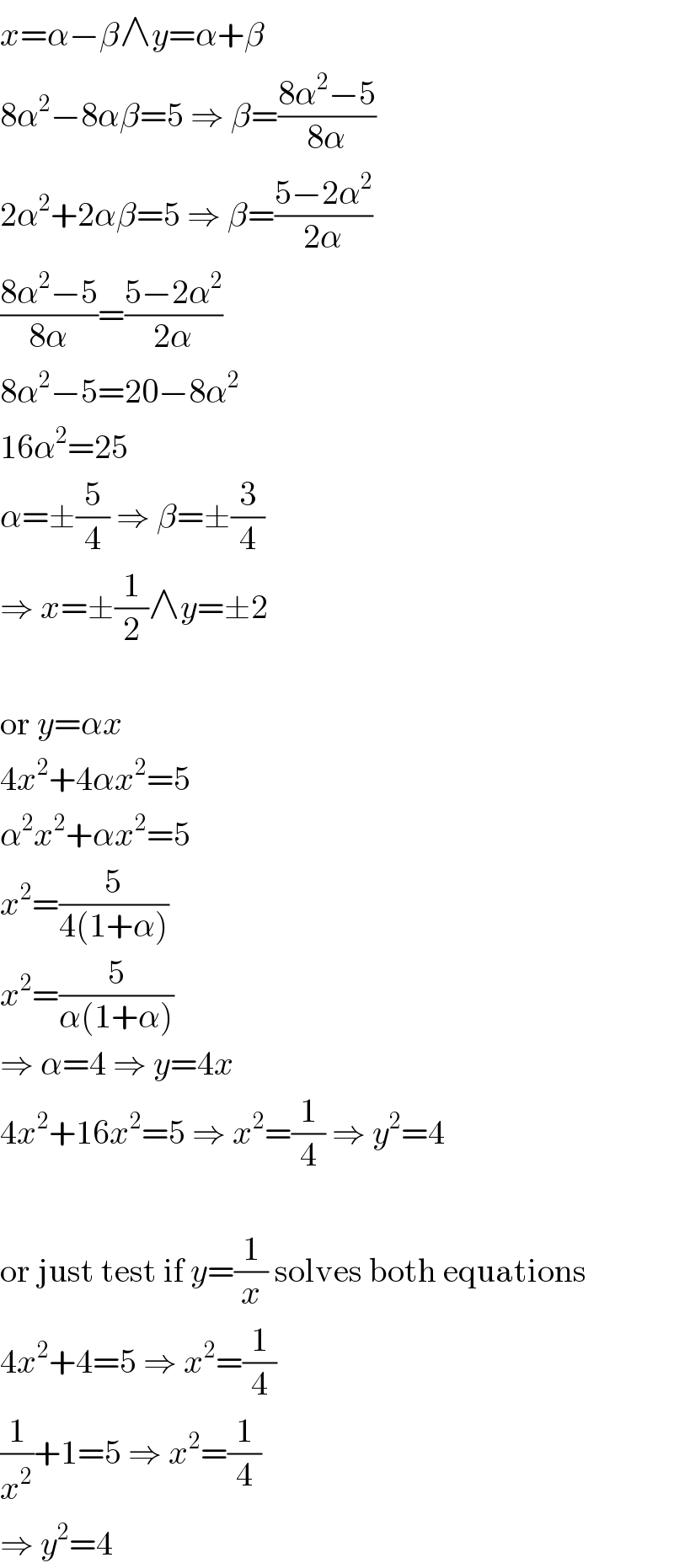
x=α−β∧y=α+β 8α^2 −8αβ=5 ⇒ β=((8α^2 −5)/(8α)) 2α^2 +2αβ=5 ⇒ β=((5−2α^2 )/(2α)) ((8α^2 −5)/(8α))=((5−2α^2 )/(2α)) 8α^2 −5=20−8α^2 16α^2 =25 α=±(5/4) ⇒ β=±(3/4) ⇒ x=±(1/2)∧y=±2 or y=αx 4x^2 +4αx^2 =5 α^2 x^2 +αx^2 =5 x^2 =(5/(4(1+α))) x^2 =(5/(α(1+α))) ⇒ α=4 ⇒ y=4x 4x^2 +16x^2 =5 ⇒ x^2 =(1/4) ⇒ y^2 =4 or just test if y=(1/x) solves both equations 4x^2 +4=5 ⇒ x^2 =(1/4) (1/x^2 )+1=5 ⇒ x^2 =(1/4) ⇒ y^2 =4

$${x}=\alpha−\beta\wedge{y}=\alpha+\beta \\ $$$$\mathrm{8}\alpha^{\mathrm{2}} −\mathrm{8}\alpha\beta=\mathrm{5}\:\Rightarrow\:\beta=\frac{\mathrm{8}\alpha^{\mathrm{2}} −\mathrm{5}}{\mathrm{8}\alpha} \\ $$$$\mathrm{2}\alpha^{\mathrm{2}} +\mathrm{2}\alpha\beta=\mathrm{5}\:\Rightarrow\:\beta=\frac{\mathrm{5}−\mathrm{2}\alpha^{\mathrm{2}} }{\mathrm{2}\alpha} \\ $$$$\frac{\mathrm{8}\alpha^{\mathrm{2}} −\mathrm{5}}{\mathrm{8}\alpha}=\frac{\mathrm{5}−\mathrm{2}\alpha^{\mathrm{2}} }{\mathrm{2}\alpha} \\ $$$$\mathrm{8}\alpha^{\mathrm{2}} −\mathrm{5}=\mathrm{20}−\mathrm{8}\alpha^{\mathrm{2}} \\ $$$$\mathrm{16}\alpha^{\mathrm{2}} =\mathrm{25} \\ $$$$\alpha=\pm\frac{\mathrm{5}}{\mathrm{4}}\:\Rightarrow\:\beta=\pm\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\Rightarrow\:{x}=\pm\frac{\mathrm{1}}{\mathrm{2}}\wedge{y}=\pm\mathrm{2} \\ $$$$ \\ $$$$\mathrm{or}\:{y}=\alpha{x} \\ $$$$\mathrm{4}{x}^{\mathrm{2}} +\mathrm{4}\alpha{x}^{\mathrm{2}} =\mathrm{5} \\ $$$$\alpha^{\mathrm{2}} {x}^{\mathrm{2}} +\alpha{x}^{\mathrm{2}} =\mathrm{5} \\ $$$${x}^{\mathrm{2}} =\frac{\mathrm{5}}{\mathrm{4}\left(\mathrm{1}+\alpha\right)} \\ $$$${x}^{\mathrm{2}} =\frac{\mathrm{5}}{\alpha\left(\mathrm{1}+\alpha\right)} \\ $$$$\Rightarrow\:\alpha=\mathrm{4}\:\Rightarrow\:{y}=\mathrm{4}{x} \\ $$$$\mathrm{4}{x}^{\mathrm{2}} +\mathrm{16}{x}^{\mathrm{2}} =\mathrm{5}\:\Rightarrow\:{x}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow\:{y}^{\mathrm{2}} =\mathrm{4} \\ $$$$ \\ $$$$\mathrm{or}\:\mathrm{just}\:\mathrm{test}\:\mathrm{if}\:{y}=\frac{\mathrm{1}}{{x}}\:\mathrm{solves}\:\mathrm{both}\:\mathrm{equations} \\ $$$$\mathrm{4}{x}^{\mathrm{2}} +\mathrm{4}=\mathrm{5}\:\Rightarrow\:{x}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{1}=\mathrm{5}\:\Rightarrow\:{x}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow\:{y}^{\mathrm{2}} =\mathrm{4} \\ $$

Answered by 1549442205PVT last updated on 14/Aug/20

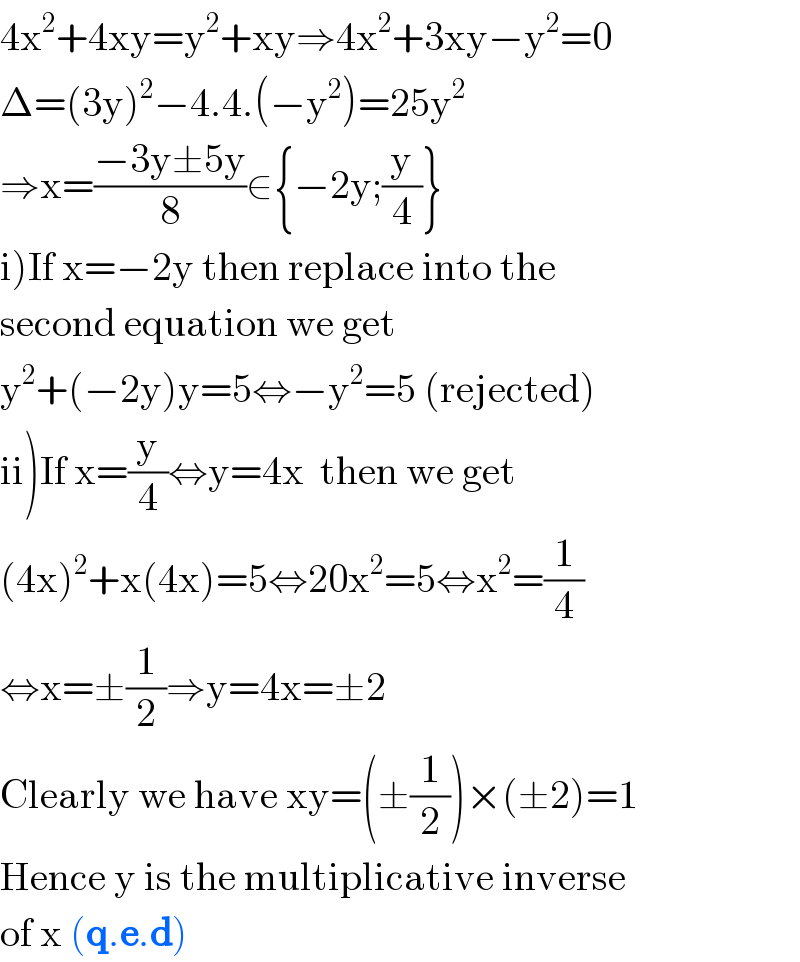
4x^2 +4xy=y^2 +xy⇒4x^2 +3xy−y^2 =0 Δ=(3y)^2 −4.4.(−y^2 )=25y^2 ⇒x=((−3y±5y)/8)∈{−2y;(y/4)} i)If x=−2y then replace into the second equation we get y^2 +(−2y)y=5⇔−y^2 =5 (rejected) ii)If x=(y/4)⇔y=4x then we get (4x)^2 +x(4x)=5⇔20x^2 =5⇔x^2 =(1/4) ⇔x=±(1/2)⇒y=4x=±2 Clearly we have xy=(±(1/2))×(±2)=1 Hence y is the multiplicative inverse of x (q.e.d)

$$\mathrm{4x}^{\mathrm{2}} +\mathrm{4xy}=\mathrm{y}^{\mathrm{2}} +\mathrm{xy}\Rightarrow\mathrm{4x}^{\mathrm{2}} +\mathrm{3xy}−\mathrm{y}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Delta=\left(\mathrm{3y}\right)^{\mathrm{2}} −\mathrm{4}.\mathrm{4}.\left(−\mathrm{y}^{\mathrm{2}} \right)=\mathrm{25y}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{x}=\frac{−\mathrm{3y}\pm\mathrm{5y}}{\mathrm{8}}\in\left\{−\mathrm{2y};\frac{\mathrm{y}}{\mathrm{4}}\right\} \\ $$$$\left.\mathrm{i}\right)\mathrm{If}\:\mathrm{x}=−\mathrm{2y}\:\mathrm{then}\:\mathrm{replace}\:\mathrm{into}\:\mathrm{the} \\ $$$$\mathrm{second}\:\mathrm{equation}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{y}^{\mathrm{2}} +\left(−\mathrm{2y}\right)\mathrm{y}=\mathrm{5}\Leftrightarrow−\mathrm{y}^{\mathrm{2}} =\mathrm{5}\:\left(\mathrm{rejected}\right) \\ $$$$\left.\mathrm{ii}\right)\mathrm{If}\:\mathrm{x}=\frac{\mathrm{y}}{\mathrm{4}}\Leftrightarrow\mathrm{y}=\mathrm{4x}\:\:\mathrm{then}\:\mathrm{we}\:\mathrm{get} \\ $$$$\left(\mathrm{4x}\right)^{\mathrm{2}} +\mathrm{x}\left(\mathrm{4x}\right)=\mathrm{5}\Leftrightarrow\mathrm{20x}^{\mathrm{2}} =\mathrm{5}\Leftrightarrow\mathrm{x}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Leftrightarrow\mathrm{x}=\pm\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\mathrm{y}=\mathrm{4x}=\pm\mathrm{2} \\ $$$$\mathrm{Clearly}\:\mathrm{we}\:\mathrm{have}\:\mathrm{xy}=\left(\pm\frac{\mathrm{1}}{\mathrm{2}}\right)×\left(\pm\mathrm{2}\right)=\mathrm{1} \\ $$$$\mathrm{Hence}\:\mathrm{y}\:\mathrm{is}\:\mathrm{the}\:\mathrm{multiplicative}\:\mathrm{inverse} \\ $$$$\mathrm{of}\:\mathrm{x}\:\left(\boldsymbol{\mathrm{q}}.\boldsymbol{\mathrm{e}}.\boldsymbol{\mathrm{d}}\right) \\ $$

Commented by Don08q last updated on 14/Aug/20

Thanks Sir

$${Thanks}\:{Sir} \\ $$

Answered by Rasheed.Sindhi last updated on 14/Aug/20

y is inverse of x⇒xy=1.So now the question in other words is: “To show the following system consistent ”: { ((4x^2 +4xy=5)),((y^2 +xy=5)),((xy=1)) :} I-E the system has common solution. ⇒ { ((4x^2 +4(1)=5⇒x=±(1/2))),((y^2 +(1)=5⇒y=±2)) :} Since ((1/2),2) & (−(1/2),−2) are solutions satisfying the system so the system is consistent. (Evident from solutions that y is multiplicative inverse of x.)

$${y}\:{is}\:{inverse}\:{of}\:{x}\Rightarrow{xy}=\mathrm{1}.\mathrm{So}\:\mathrm{now} \\ $$$$\mathrm{the}\:\mathrm{question}\:\mathrm{in}\:\mathrm{other}\:\mathrm{words}\:\mathrm{is}: \\ $$$$``{To}\:{show}\:{the}\:{following}\:{system} \\ $$$$\:\:\:\boldsymbol{{consistent}}\:'': \\ $$$$\:\begin{cases}{\mathrm{4}{x}^{\mathrm{2}} +\mathrm{4}{xy}=\mathrm{5}}\\{{y}^{\mathrm{2}} +{xy}=\mathrm{5}}\\{{xy}=\mathrm{1}}\end{cases} \\ $$$${I}-{E}\:\:{the}\:{system}\:{has}\:{common}\: \\ $$$${solution}. \\ $$$$\:\Rightarrow\begin{cases}{\mathrm{4}{x}^{\mathrm{2}} +\mathrm{4}\left(\mathrm{1}\right)=\mathrm{5}\Rightarrow{x}=\pm\frac{\mathrm{1}}{\mathrm{2}}}\\{{y}^{\mathrm{2}} +\left(\mathrm{1}\right)=\mathrm{5}\Rightarrow{y}=\pm\mathrm{2}}\end{cases} \\ $$$${Since}\:\left(\frac{\mathrm{1}}{\mathrm{2}},\mathrm{2}\right)\:\&\:\left(−\frac{\mathrm{1}}{\mathrm{2}},−\mathrm{2}\right)\:{are} \\ $$$${solutions}\:{satisfying}\:{the}\:{system} \\ $$$${so}\:{the}\:{system}\:{is}\:\boldsymbol{{consistent}}. \\ $$$$\left({Evident}\:{from}\:{solutions}\:{that}\right. \\ $$$$\left.{y}\:{is}\:{multiplicative}\:{inverse}\:{of}\:{x}.\right) \\ $$

Commented by Don08q last updated on 14/Aug/20

Thanks Sir

$${Thanks}\:{Sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com