
Question Number 107779 by ajfour last updated on 12/Aug/20
Commented by ajfour last updated on 12/Aug/20
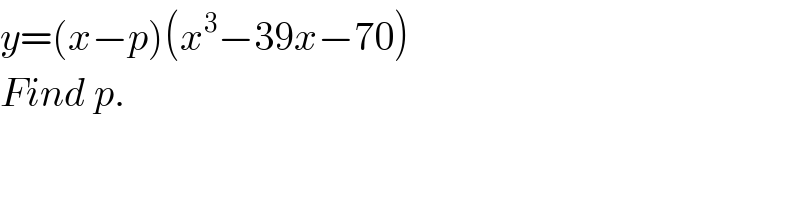
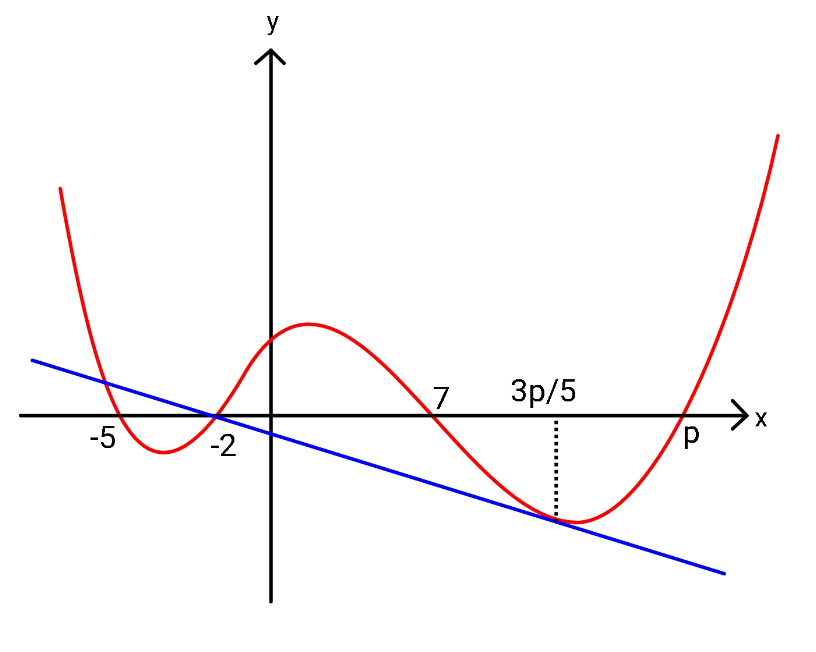
$${y}=\left({x}−{p}\right)\left({x}^{\mathrm{3}} −\mathrm{39}{x}−\mathrm{70}\right) \\ $$$${Find}\:{p}. \\ $$
Commented by Sarah85 last updated on 12/Aug/20
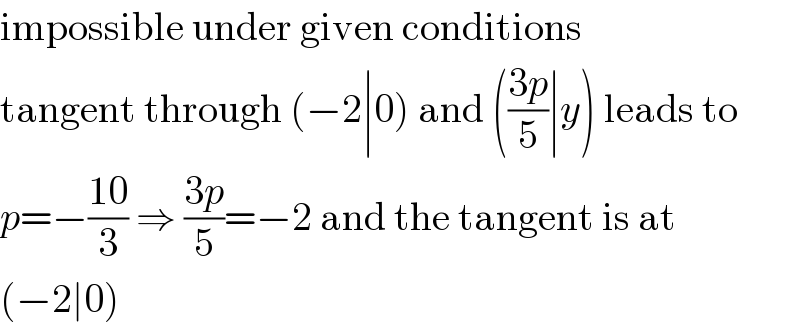
$$\mathrm{impossible}\:\mathrm{under}\:\mathrm{given}\:\mathrm{conditions} \\ $$$$\mathrm{tangent}\:\mathrm{through}\:\left(−\mathrm{2}\mid\mathrm{0}\right)\:\mathrm{and}\:\left(\frac{\mathrm{3}{p}}{\mathrm{5}}\mid{y}\right)\:\mathrm{leads}\:\mathrm{to} \\ $$$${p}=−\frac{\mathrm{10}}{\mathrm{3}}\:\Rightarrow\:\frac{\mathrm{3}{p}}{\mathrm{5}}=−\mathrm{2}\:\mathrm{and}\:\mathrm{the}\:\mathrm{tangent}\:\mathrm{is}\:\mathrm{at} \\ $$$$\left(−\mathrm{2}\mid\mathrm{0}\right) \\ $$
Commented by ajfour last updated on 13/Aug/20

$${thanks}\:{anyway}.. \\ $$
Answered by floor(10²Eta[1]) last updated on 13/Aug/20
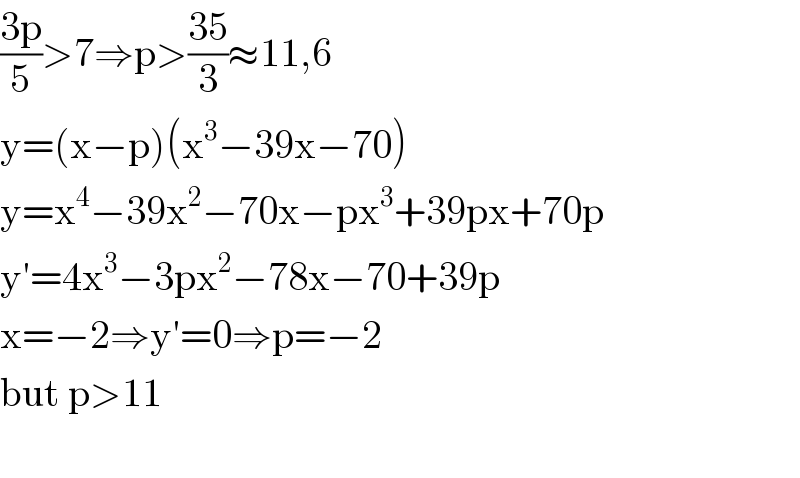
$$\frac{\mathrm{3p}}{\mathrm{5}}>\mathrm{7}\Rightarrow\mathrm{p}>\frac{\mathrm{35}}{\mathrm{3}}\approx\mathrm{11},\mathrm{6} \\ $$$$\mathrm{y}=\left(\mathrm{x}−\mathrm{p}\right)\left(\mathrm{x}^{\mathrm{3}} −\mathrm{39x}−\mathrm{70}\right) \\ $$$$\mathrm{y}=\mathrm{x}^{\mathrm{4}} −\mathrm{39x}^{\mathrm{2}} −\mathrm{70x}−\mathrm{px}^{\mathrm{3}} +\mathrm{39px}+\mathrm{70p} \\ $$$$\mathrm{y}'=\mathrm{4x}^{\mathrm{3}} −\mathrm{3px}^{\mathrm{2}} −\mathrm{78x}−\mathrm{70}+\mathrm{39p} \\ $$$$\mathrm{x}=−\mathrm{2}\Rightarrow\mathrm{y}'=\mathrm{0}\Rightarrow\mathrm{p}=−\mathrm{2} \\ $$$$\mathrm{but}\:\mathrm{p}>\mathrm{11}\: \\ $$$$ \\ $$
Commented by Sarah85 last updated on 13/Aug/20
$$\mathrm{that}'\mathrm{s}\:\mathrm{what}\:\mathrm{I}\:\mathrm{wrote}\:\mathrm{before} \\ $$
