
Question Number 107609 by mathdave last updated on 11/Aug/20

Answered by mr W last updated on 11/Aug/20
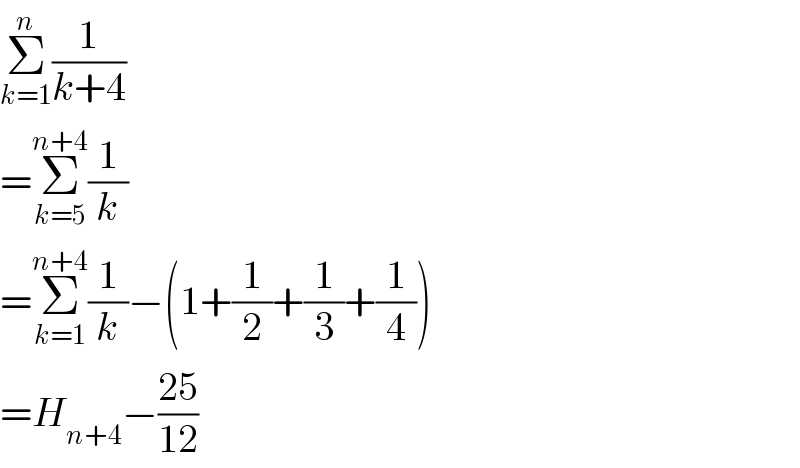
$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{k}+\mathrm{4}} \\ $$$$=\underset{{k}=\mathrm{5}} {\overset{{n}+\mathrm{4}} {\sum}}\frac{\mathrm{1}}{{k}} \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{{n}+\mathrm{4}} {\sum}}\frac{\mathrm{1}}{{k}}−\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$$={H}_{{n}+\mathrm{4}} −\frac{\mathrm{25}}{\mathrm{12}} \\ $$
Commented by mathdave last updated on 11/Aug/20
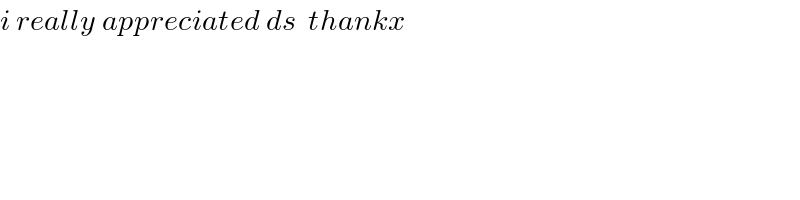
$${i}\:{really}\:{appreciated}\:{ds}\:\:{thankx} \\ $$
Answered by hgrocks last updated on 11/Aug/20
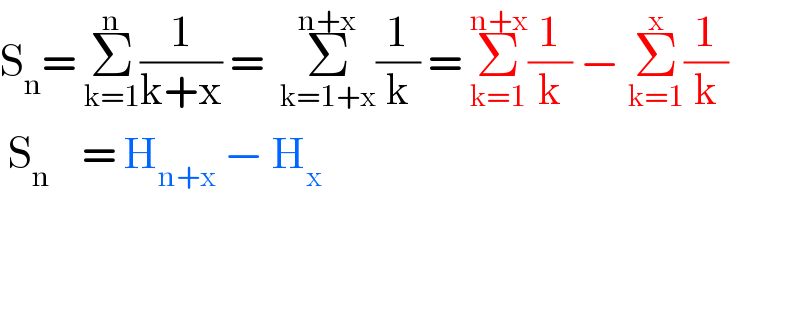
$$\mathrm{S}_{\mathrm{n}} =\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{k}+\mathrm{x}}\:=\:\:\underset{\mathrm{k}=\mathrm{1}+\mathrm{x}} {\overset{\mathrm{n}+\mathrm{x}} {\sum}}\frac{\mathrm{1}}{\mathrm{k}}\:=\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}+\mathrm{x}} {\sum}}\frac{\mathrm{1}}{\mathrm{k}}\:−\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{x}} {\sum}}\frac{\mathrm{1}}{\mathrm{k}} \\ $$$$\:\mathrm{S}_{\mathrm{n}} \:\:\:\:=\:\mathrm{H}_{\mathrm{n}+\mathrm{x}} \:−\:\mathrm{H}_{\mathrm{x}} \\ $$$$ \\ $$$$ \\ $$
Commented by mathdave last updated on 11/Aug/20

$${thank}\:{so}\:{so}\:{much} \\ $$
