Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 106727 by Algoritm last updated on 06/Aug/20

Answered by Her_Majesty last updated on 06/Aug/20

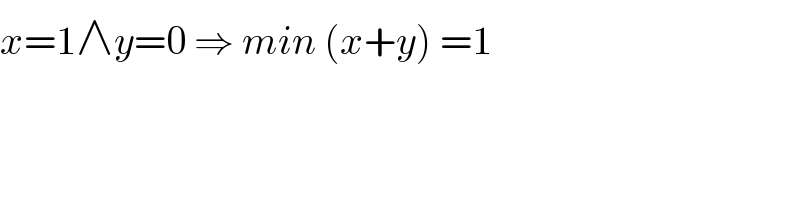
x=1∧y=0 ⇒ min (x+y) =1

$${x}=\mathrm{1}\wedge{y}=\mathrm{0}\:\Rightarrow\:{min}\:\left({x}+{y}\right)\:=\mathrm{1} \\ $$

Commented by Her_Majesty last updated on 06/Aug/20

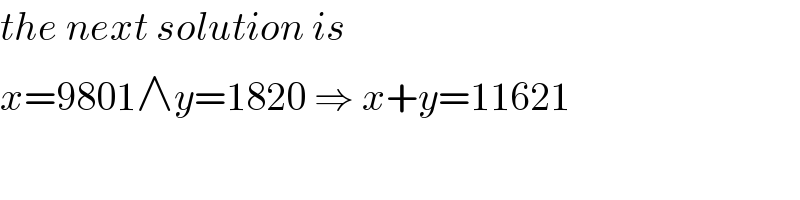
the next solution is x=9801∧y=1820 ⇒ x+y=11621

$${the}\:{next}\:{solution}\:{is} \\ $$$${x}=\mathrm{9801}\wedge{y}=\mathrm{1820}\:\Rightarrow\:{x}+{y}=\mathrm{11621} \\ $$

Commented by mathmax by abdo last updated on 07/Aug/20

can you show the work ...

$$\mathrm{can}\:\mathrm{you}\:\mathrm{show}\:\mathrm{the}\:\mathrm{work}\:... \\ $$

Commented by Her_Majesty last updated on 07/Aug/20

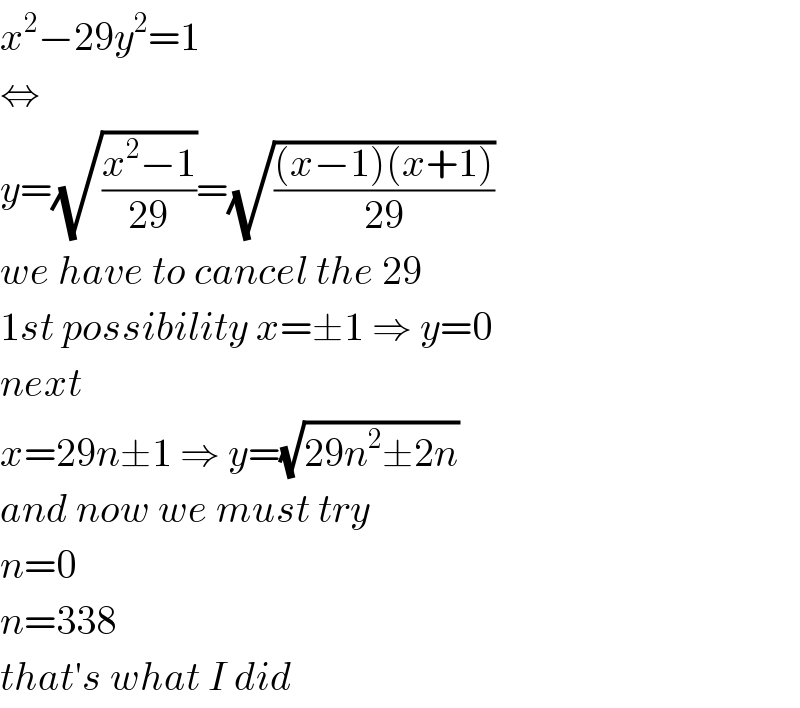
x^2 −29y^2 =1 ⇔ y=(√((x^2 −1)/(29)))=(√(((x−1)(x+1))/(29))) we have to cancel the 29 1st possibility x=±1 ⇒ y=0 next x=29n±1 ⇒ y=(√(29n^2 ±2n)) and now we must try n=0 n=338 that′s what I did

$${x}^{\mathrm{2}} −\mathrm{29}{y}^{\mathrm{2}} =\mathrm{1} \\ $$$$\Leftrightarrow \\ $$$${y}=\sqrt{\frac{{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{29}}}=\sqrt{\frac{\left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)}{\mathrm{29}}} \\ $$$${we}\:{have}\:{to}\:{cancel}\:{the}\:\mathrm{29} \\ $$$$\mathrm{1}{st}\:{possibility}\:{x}=\pm\mathrm{1}\:\Rightarrow\:{y}=\mathrm{0} \\ $$$${next} \\ $$$${x}=\mathrm{29}{n}\pm\mathrm{1}\:\Rightarrow\:{y}=\sqrt{\mathrm{29}{n}^{\mathrm{2}} \pm\mathrm{2}{n}} \\ $$$${and}\:{now}\:{we}\:{must}\:{try} \\ $$$${n}=\mathrm{0} \\ $$$${n}=\mathrm{338} \\ $$$${that}'{s}\:{what}\:{I}\:{did} \\ $$

Answered by mathmax by abdo last updated on 06/Aug/20

i have a way but i cant complete it that nead calculus 29 is prime so we considere congruence modulo 29 x^2 −29y^2 =1 ⇒x^−^2 −0 =1^− ⇒(x^− −1)(x^− +1) =0 ⇒x^− =1 or x^− =−1 (Z/29Z)is a corps case 1 x^− =1 ⇒ x =29k +1 x^2 −29y^2 =1 ⇒(29k+1)^2 −29y^2 =1 ⇒29^2 k^2 +2.29k +1−29y^2 =1 ⇒29k^2 +2k−y^2 =0 ⇒y^2 =29k^2 +2k ⇒y =(√(29k^2 +2k)) so we seark all integr k /29k^2 +2k =m^(2 ) we verify with k=0 ,1 ,2 ,3,4....be continued...

$$\mathrm{i}\:\mathrm{have}\:\mathrm{a}\:\mathrm{way}\:\mathrm{but}\:\mathrm{i}\:\mathrm{cant}\:\mathrm{complete}\:\mathrm{it}\:\mathrm{that}\:\mathrm{nead}\:\:\mathrm{calculus} \\ $$$$\mathrm{29}\:\mathrm{is}\:\mathrm{prime}\:\mathrm{so}\:\mathrm{we}\:\mathrm{considere}\:\mathrm{congruence}\:\mathrm{modulo}\:\mathrm{29} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{29y}^{\mathrm{2}} \:=\mathrm{1}\:\Rightarrow\overset{−^{\mathrm{2}} } {\mathrm{x}}−\mathrm{0}\:=\overset{−} {\mathrm{1}}\:\Rightarrow\left(\overset{−} {\mathrm{x}}−\mathrm{1}\right)\left(\overset{−} {\mathrm{x}}+\mathrm{1}\right)\:=\mathrm{0}\:\Rightarrow\overset{−} {\mathrm{x}}\:=\mathrm{1}\:\mathrm{or}\:\overset{−} {\mathrm{x}}\:=−\mathrm{1} \\ $$$$\left(\mathrm{Z}/\mathrm{29Z}\right)\mathrm{is}\:\mathrm{a}\:\mathrm{corps}\:\mathrm{case}\:\mathrm{1}\:\overset{−} {\mathrm{x}}=\mathrm{1}\:\Rightarrow\:\mathrm{x}\:=\mathrm{29k}\:+\mathrm{1} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{29y}^{\mathrm{2}} \:=\mathrm{1}\:\Rightarrow\left(\mathrm{29k}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{29y}^{\mathrm{2}} \:=\mathrm{1}\:\Rightarrow\mathrm{29}^{\mathrm{2}} \mathrm{k}^{\mathrm{2}} \:+\mathrm{2}.\mathrm{29k}\:+\mathrm{1}−\mathrm{29y}^{\mathrm{2}} \:=\mathrm{1} \\ $$$$\Rightarrow\mathrm{29k}^{\mathrm{2}} \:+\mathrm{2k}−\mathrm{y}^{\mathrm{2}} \:=\mathrm{0}\:\Rightarrow\mathrm{y}^{\mathrm{2}} \:=\mathrm{29k}^{\mathrm{2}} \:+\mathrm{2k}\:\Rightarrow\mathrm{y}\:=\sqrt{\mathrm{29k}^{\mathrm{2}} \:+\mathrm{2k}} \\ $$$$\mathrm{so}\:\mathrm{we}\:\mathrm{seark}\:\mathrm{all}\:\mathrm{integr}\:\mathrm{k}\:/\mathrm{29k}^{\mathrm{2}} \:+\mathrm{2k}\:=\mathrm{m}^{\mathrm{2}\:} \\ $$$$\mathrm{we}\:\mathrm{verify}\:\mathrm{with}\:\mathrm{k}=\mathrm{0}\:,\mathrm{1}\:,\mathrm{2}\:,\mathrm{3},\mathrm{4}....\mathrm{be}\:\mathrm{continued}... \\ $$$$ \\ $$

Commented by Algoritm last updated on 07/Aug/20

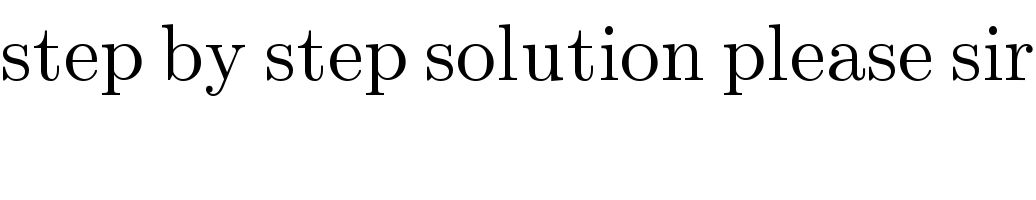
step by step solution please sir

$$\mathrm{step}\:\mathrm{by}\:\mathrm{step}\:\mathrm{solution}\:\mathrm{please}\:\mathrm{sir} \\ $$

Commented by Her_Majesty last updated on 07/Aug/20

are you blind?

$${are}\:{you}\:{blind}? \\ $$

Commented by Rasheed.Sindhi last updated on 07/Aug/20

We can′t expect any harsh comment from a graceful personality such as yours!!!

$${We}\:{can}'{t}\:{expect}\:{any}\:{harsh} \\ $$$${comment}\:{from}\:{a}\:{graceful}\: \\ $$$${personality}\:{such}\:{as}\:{yours}!!! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com