Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 106449 by mohammad17 last updated on 05/Aug/20

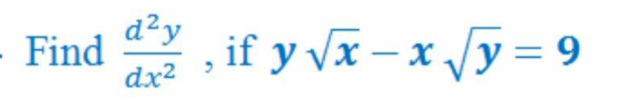
Answered by Dwaipayan Shikari last updated on 05/Aug/20

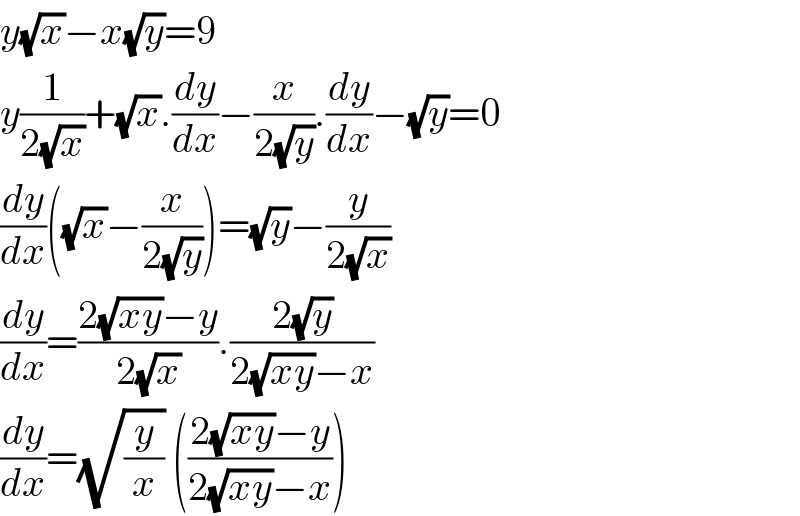
y(√x)−x(√y)=9 y(1/(2(√x)))+(√x).(dy/dx)−(x/(2(√y))).(dy/dx)−(√y)=0 (dy/dx)((√x)−(x/(2(√y))))=(√y)−(y/(2(√x))) (dy/dx)=((2(√(xy))−y)/(2(√x))).((2(√y))/(2(√(xy))−x)) (dy/dx)=(√(y/x)) (((2(√(xy))−y)/(2(√(xy))−x)))

$${y}\sqrt{{x}}−{x}\sqrt{{y}}=\mathrm{9} \\ $$$${y}\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}+\sqrt{{x}}.\frac{{dy}}{{dx}}−\frac{{x}}{\mathrm{2}\sqrt{{y}}}.\frac{{dy}}{{dx}}−\sqrt{{y}}=\mathrm{0} \\ $$$$\frac{{dy}}{{dx}}\left(\sqrt{{x}}−\frac{{x}}{\mathrm{2}\sqrt{{y}}}\right)=\sqrt{{y}}−\frac{{y}}{\mathrm{2}\sqrt{{x}}} \\ $$$$\frac{{dy}}{{dx}}=\frac{\mathrm{2}\sqrt{{xy}}−{y}}{\mathrm{2}\sqrt{{x}}}.\frac{\mathrm{2}\sqrt{{y}}}{\mathrm{2}\sqrt{{xy}}−{x}} \\ $$$$\frac{{dy}}{{dx}}=\sqrt{\frac{{y}}{{x}}}\:\left(\frac{\mathrm{2}\sqrt{{xy}}−{y}}{\mathrm{2}\sqrt{{xy}}−{x}}\right) \\ $$

Commented by mohammad17 last updated on 05/Aug/20

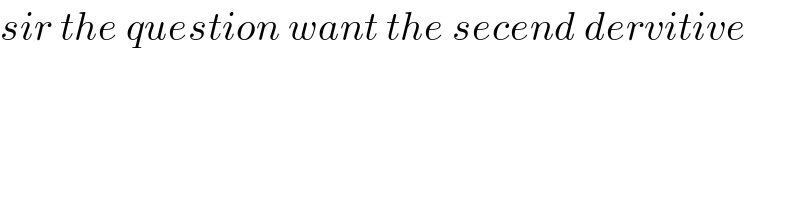
sir the question want the secend dervitive

$${sir}\:{the}\:{question}\:{want}\:{the}\:{secend}\:{dervitive} \\ $$

Answered by Dwaipayan Shikari last updated on 05/Aug/20

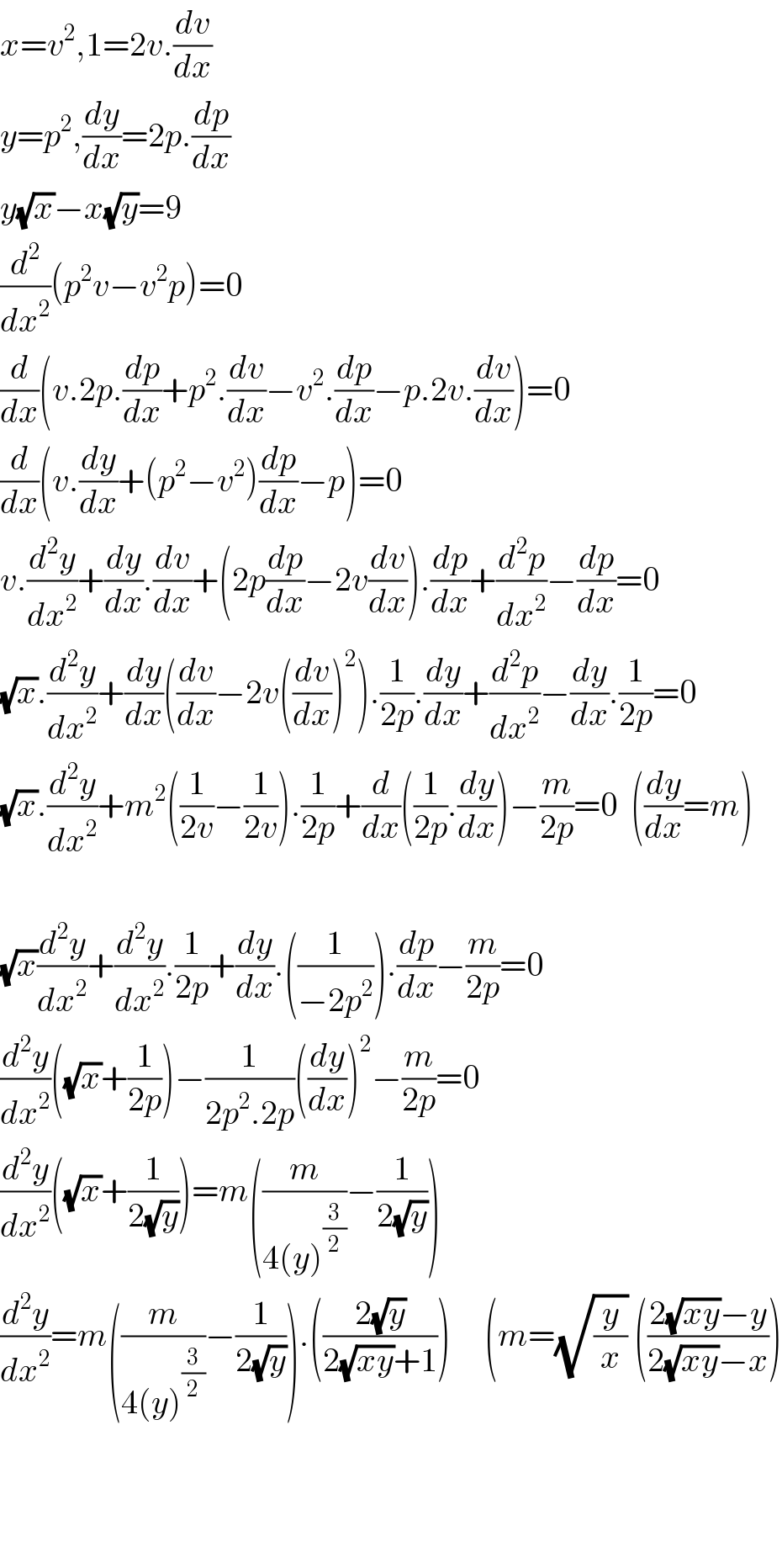
x=v^2 ,1=2v.(dv/dx) y=p^2 ,(dy/dx)=2p.(dp/dx) y(√x)−x(√y)=9 (d^2 /dx^2 )(p^2 v−v^2 p)=0 (d/dx)(v.2p.(dp/dx)+p^2 .(dv/dx)−v^2 .(dp/dx)−p.2v.(dv/dx))=0 (d/dx)(v.(dy/dx)+(p^2 −v^2 )(dp/dx)−p)=0 v.(d^2 y/dx^2 )+(dy/dx).(dv/dx)+(2p(dp/dx)−2v(dv/dx)).(dp/dx)+(d^2 p/dx^2 )−(dp/dx)=0 (√x).(d^2 y/dx^2 )+(dy/dx)((dv/dx)−2v((dv/dx))^2 ).(1/(2p)).(dy/dx)+(d^2 p/dx^2 )−(dy/dx).(1/(2p))=0 (√x).(d^2 y/dx^2 )+m^2 ((1/(2v))−(1/(2v))).(1/(2p))+(d/dx)((1/(2p)).(dy/dx))−(m/(2p))=0 ((dy/dx)=m) (√x)(d^2 y/dx^2 )+(d^2 y/dx^2 ).(1/(2p))+(dy/dx).((1/(−2p^2 ))).(dp/dx)−(m/(2p))=0 (d^2 y/dx^2 )((√x)+(1/(2p)))−(1/(2p^2 .2p))((dy/dx))^2 −(m/(2p))=0 (d^2 y/dx^2 )((√x)+(1/(2(√y))))=m((m/(4(y)^(3/2) ))−(1/(2(√y)))) (d^2 y/dx^2 )=m((m/(4(y)^(3/2) ))−(1/(2(√y)))).(((2(√y))/(2(√(xy))+1))) (m=(√(y/x)) (((2(√(xy))−y)/(2(√(xy))−x)))

$${x}={v}^{\mathrm{2}} ,\mathrm{1}=\mathrm{2}{v}.\frac{{dv}}{{dx}} \\ $$$${y}={p}^{\mathrm{2}} ,\frac{{dy}}{{dx}}=\mathrm{2}{p}.\frac{{dp}}{{dx}} \\ $$$${y}\sqrt{{x}}−{x}\sqrt{{y}}=\mathrm{9} \\ $$$$\frac{{d}^{\mathrm{2}} }{{dx}^{\mathrm{2}} }\left({p}^{\mathrm{2}} {v}−{v}^{\mathrm{2}} {p}\right)=\mathrm{0} \\ $$$$\frac{{d}}{{dx}}\left({v}.\mathrm{2}{p}.\frac{{dp}}{{dx}}+{p}^{\mathrm{2}} .\frac{{dv}}{{dx}}−{v}^{\mathrm{2}} .\frac{{dp}}{{dx}}−{p}.\mathrm{2}{v}.\frac{{dv}}{{dx}}\right)=\mathrm{0} \\ $$$$\frac{{d}}{{dx}}\left({v}.\frac{{dy}}{{dx}}+\left({p}^{\mathrm{2}} −{v}^{\mathrm{2}} \right)\frac{{dp}}{{dx}}−{p}\right)=\mathrm{0} \\ $$$${v}.\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }+\frac{{dy}}{{dx}}.\frac{{dv}}{{dx}}+\left(\mathrm{2}{p}\frac{{dp}}{{dx}}−\mathrm{2}{v}\frac{{dv}}{{dx}}\right).\frac{{dp}}{{dx}}+\frac{{d}^{\mathrm{2}} {p}}{{dx}^{\mathrm{2}} }−\frac{{dp}}{{dx}}=\mathrm{0} \\ $$$$\sqrt{{x}}.\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }+\frac{{dy}}{{dx}}\left(\frac{{dv}}{{dx}}−\mathrm{2}{v}\left(\frac{{dv}}{{dx}}\right)^{\mathrm{2}} \right).\frac{\mathrm{1}}{\mathrm{2}{p}}.\frac{{dy}}{{dx}}+\frac{{d}^{\mathrm{2}} {p}}{{dx}^{\mathrm{2}} }−\frac{{dy}}{{dx}}.\frac{\mathrm{1}}{\mathrm{2}{p}}=\mathrm{0} \\ $$$$\sqrt{{x}}.\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }+{m}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}{v}}−\frac{\mathrm{1}}{\mathrm{2}{v}}\right).\frac{\mathrm{1}}{\mathrm{2}{p}}+\frac{{d}}{{dx}}\left(\frac{\mathrm{1}}{\mathrm{2}{p}}.\frac{{dy}}{{dx}}\right)−\frac{{m}}{\mathrm{2}{p}}=\mathrm{0}\:\:\left(\frac{{dy}}{{dx}}={m}\right) \\ $$$$ \\ $$$$\sqrt{{x}}\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }+\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }.\frac{\mathrm{1}}{\mathrm{2}{p}}+\frac{{dy}}{{dx}}.\left(\frac{\mathrm{1}}{−\mathrm{2}{p}^{\mathrm{2}} }\right).\frac{{dp}}{{dx}}−\frac{{m}}{\mathrm{2}{p}}=\mathrm{0} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\left(\sqrt{{x}}+\frac{\mathrm{1}}{\mathrm{2}{p}}\right)−\frac{\mathrm{1}}{\mathrm{2}{p}^{\mathrm{2}} .\mathrm{2}{p}}\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} −\frac{{m}}{\mathrm{2}{p}}=\mathrm{0} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\left(\sqrt{{x}}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{{y}}}\right)={m}\left(\frac{{m}}{\mathrm{4}\left({y}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }−\frac{\mathrm{1}}{\mathrm{2}\sqrt{{y}}}\right) \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }={m}\left(\frac{{m}}{\mathrm{4}\left({y}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }−\frac{\mathrm{1}}{\mathrm{2}\sqrt{{y}}}\right).\left(\frac{\mathrm{2}\sqrt{{y}}}{\mathrm{2}\sqrt{{xy}}+\mathrm{1}}\right)\:\:\:\:\:\left({m}=\sqrt{\frac{{y}}{{x}}}\:\left(\frac{\mathrm{2}\sqrt{{xy}}−{y}}{\mathrm{2}\sqrt{{xy}}−{x}}\right)\right. \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Answered by mathmax by abdo last updated on 05/Aug/20

in this case is better to use bospital rule let u(x) =1−cos(4x)sin^2 (x)−cos^2 (x) and v(x)=x^4 ⇒ u(x) =1−cos(4x)(((1−cos(2x))/2))−((1+cos(2x))/2) =(1/2)−(1/2)cos(4x)+(1/2)cos(4x)cos(2x)−(1/2)cos(2x) =(1/2)−(1/2)cos(2x)−(1/2)cos(4x)+(1/4)(cos(6x)+cos(2x)) =(1/2)−(1/4)cos(2x)−(1/2)cos(4x)+(1/4)cos(6x) ⇒ u^′ (x) =(1/2)sin(2x)+2sin(4x)−(3/2)sin(6x) u^((2)) (x) =cos(2x)+8cos(4x)−9cos(6x) u^((3)) (x) =−2sin(2x)−32sin(4x) +54 sin(6x) u^((4)) (x) =−4cos(2x)−128 cos(4x)+6×54cos(6x) ⇒lim_(x→0) u^((4)) (x) =−4−128 +6×54 =54×6−132 =324−132 =192 v^′ (x) =4x^3 ⇒v^((2)) (x) =12x^2 ⇒v^((3)) (x) =24 x ⇒v^((4)) (x) =24 ⇒lim_(x→0) ((u(x))/(v(x))) =((192)/(24))

$$\mathrm{in}\:\mathrm{this}\:\mathrm{case}\:\mathrm{is}\:\mathrm{better}\:\mathrm{to}\:\mathrm{use}\:\mathrm{bospital}\:\mathrm{rule}\:\mathrm{let} \\ $$$$\mathrm{u}\left(\mathrm{x}\right)\:=\mathrm{1}−\mathrm{cos}\left(\mathrm{4x}\right)\mathrm{sin}^{\mathrm{2}} \left(\mathrm{x}\right)−\mathrm{cos}^{\mathrm{2}} \left(\mathrm{x}\right)\:\mathrm{and}\:\mathrm{v}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{4}} \:\Rightarrow \\ $$$$\mathrm{u}\left(\mathrm{x}\right)\:=\mathrm{1}−\mathrm{cos}\left(\mathrm{4x}\right)\left(\frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{2}}\right)−\frac{\mathrm{1}+\mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\left(\mathrm{4x}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\left(\mathrm{4x}\right)\mathrm{cos}\left(\mathrm{2x}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\left(\mathrm{2x}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\left(\mathrm{2x}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\left(\mathrm{4x}\right)+\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{cos}\left(\mathrm{6x}\right)+\mathrm{cos}\left(\mathrm{2x}\right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos}\left(\mathrm{2x}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\left(\mathrm{4x}\right)+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos}\left(\mathrm{6x}\right)\:\Rightarrow \\ $$$$\mathrm{u}^{'} \left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{2x}\right)+\mathrm{2sin}\left(\mathrm{4x}\right)−\frac{\mathrm{3}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{6x}\right) \\ $$$$\mathrm{u}^{\left(\mathrm{2}\right)} \left(\mathrm{x}\right)\:=\mathrm{cos}\left(\mathrm{2x}\right)+\mathrm{8cos}\left(\mathrm{4x}\right)−\mathrm{9cos}\left(\mathrm{6x}\right) \\ $$$$\mathrm{u}^{\left(\mathrm{3}\right)} \left(\mathrm{x}\right)\:=−\mathrm{2sin}\left(\mathrm{2x}\right)−\mathrm{32sin}\left(\mathrm{4x}\right)\:+\mathrm{54}\:\mathrm{sin}\left(\mathrm{6x}\right) \\ $$$$\mathrm{u}^{\left(\mathrm{4}\right)} \left(\mathrm{x}\right)\:=−\mathrm{4cos}\left(\mathrm{2x}\right)−\mathrm{128}\:\mathrm{cos}\left(\mathrm{4x}\right)+\mathrm{6}×\mathrm{54cos}\left(\mathrm{6x}\right) \\ $$$$\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \mathrm{u}^{\left(\mathrm{4}\right)} \left(\mathrm{x}\right)\:=−\mathrm{4}−\mathrm{128}\:+\mathrm{6}×\mathrm{54}\:=\mathrm{54}×\mathrm{6}−\mathrm{132} \\ $$$$=\mathrm{324}−\mathrm{132}\:=\mathrm{192} \\ $$$$\mathrm{v}^{'} \left(\mathrm{x}\right)\:=\mathrm{4x}^{\mathrm{3}} \:\Rightarrow\mathrm{v}^{\left(\mathrm{2}\right)} \left(\mathrm{x}\right)\:=\mathrm{12x}^{\mathrm{2}} \:\Rightarrow\mathrm{v}^{\left(\mathrm{3}\right)} \left(\mathrm{x}\right)\:=\mathrm{24}\:\mathrm{x}\:\Rightarrow\mathrm{v}^{\left(\mathrm{4}\right)} \left(\mathrm{x}\right)\:=\mathrm{24} \\ $$$$\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\:\frac{\mathrm{u}\left(\mathrm{x}\right)}{\mathrm{v}\left(\mathrm{x}\right)}\:=\frac{\mathrm{192}}{\mathrm{24}} \\ $$

Commented by mathmax by abdo last updated on 05/Aug/20

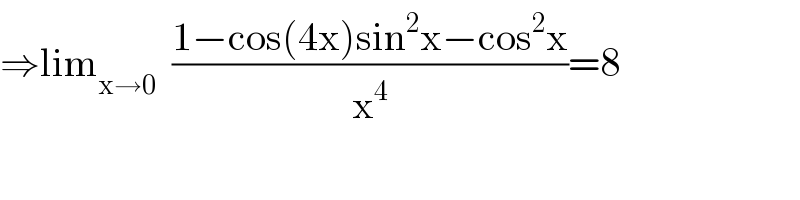
⇒lim_(x→0) ((1−cos(4x)sin^2 x−cos^2 x)/x^4 )=8

$$\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\:\frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{4x}\right)\mathrm{sin}^{\mathrm{2}} \mathrm{x}−\mathrm{cos}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}^{\mathrm{4}} }=\mathrm{8} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com